Implementing MD5 in AWK

It is only recently that I've discovered the Advent of Code, a coding challenge happening on December (though available all year) since 2015 and it is quite unique. I've set out to solve the 2015 puzzles in AWK (you can find my solutions here). Very soon one of them required to compute (a lot of) MD5 hashes. After some research, I found out there are basically three solutions:
- Using a pipe. This is expected to be slow, relying on an external program, but very simple to implement.
- Write a dynamic extension in C or C++. This should yield very good performances, but would be limited to GNU Awk and tedious to deploy as it would require compiling.
- Implement MD5 in AWK. This is expected to be portable and very slow, but more importantly a lot of fun.
In this post I'll go through the implementation of MD5 in AWK by first writing a GNU Awk version (because of some of its features), then porting to AWK, and finally optimizing. The main challenge is that MD5 is basically a lot of bitwise operations on 32-bits integers and AWK has neither. If that sounds interesting to you, sit comfortably and read on — this is going to be a long ride.
setup()
In case you missed it I wrote all this to solve a coding challenge — for fun. Theses implementations have a lot of limitations and you should not use them for anything remotely serious (well, you should not use MD5 for anything remotely serious nowadays anyway).
Let start with a basic template that mimic the openssl md5
command output:
base.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input) { # TODO } |
The script read every lines from the files given on the command line (or
consume the standard input) and save them into the content
variable. Because we want to display the computed checksum in the same order
as given, we have to do a little dance with files and
nfiles. If you are not familiar with AWK, note that
arrays are 1-indexed. We've followed this practice for
files. Also all uninitialized variables (including array values)
are 0 by default, so we don't need to explicitly initialize
nfiles.
From now on the focus will be on the md5() function. We'll be
following the RFC
step-by-step. It include a reference implementation in C,
Md5.c, that you should also find
here. It was really
handy to print debug the intermediate states etc. Now, this implementation
has been written a long time ago and need a trivial patch:
Md5.c.patch
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | --- Md5.c.original 2017-01-14 21:00:21.894542600 +0100 +++ Md5.c 2017-01-14 21:01:02.178086795 +0100 @@ -37,8 +37,10 @@ ********************************************************************** */ +#include <stdint.h> + /* typedef a 32 bit type */ -typedef unsigned long int UINT4; +typedef uint32_t UINT4; /* Data structure for MD5 (Message Digest) computation */ typedef struct { |
massaging the input
For further processing we need the message to be represented as 32-bits words:
# convert the input into an array of bytes using ord() on each
# character.
nbytes = split(input, chars, "");
for (i = 1; i <= nbytes; i++)
bytes[i] = ord(chars[i]);
Remember that arrays are 1-indexed in AWK. Thus, chars must be
walked from 1 until nbytes included.
First, we split the input string as an array of characters. One
byte per character is assumed (ASCII) but this could work with non-ASCII text
too (you may need to LC_ALL=C because
GNU Awk is locale aware). Then, we "convert" each
character as a byte using ord(). Whereas many languages have an
ord() function AWK doesn't, but fortunately we can find an
implementation from
the GNU Awk manual.
Let's hack it a bit and we get:
# from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html
function _ord_init( i)
{
for (i = 0; i < 256; i++)
_ord_[sprintf("%c", i)] = i;
}
function ord(s)
{
# only first character is of interest
return _ord_[substr(s, 1, 1)];
}
_ord_init() deserve some clarification if you're not used to
AWK: the caller is not expected to actually provide a value for
i. All variables in AWK are global except function
parameters. i is declared as parameter only to create a
variable that is local to the function, that way _ord_init()
doesn't change the global state. While very unusual in "modern" languages
this is a very common AWK trick, so common in fact that it is documented in
the manpage:
Parameters are passed by value if scalar and by reference if array name; functions may be called recursively. Parameters are local to the function; all other variables are global. Thus local variables may be created by providing excess parameters in the function definition.
Finally, let's convert our bytes array into 32-bits words.
Remember that AWK doesn't have bitwise operators? Fortunately for us,
GNU Awk
has built-in bitwise functions.
So we'll start off with GNU Awk and then figure
out a way to implement bitwise functions later on.
# convert the array of bytes into an array of 32-bits words.
# NOTE: words is 0-indexed.
for (i = 1; i <= nbytes; i += 4) {
hi = or(lshift(bytes[i + 3], 8), bytes[i + 2]);
lo = or(lshift(bytes[i + 1], 8), bytes[i + 0]);
words[nwords++] = or(lshift(hi, 16), lo);
}
Notice that we've decided to break from the 1-index array convention of AWK
for the words array here. It will make some computation less
awkward and allow us to translate "smoothly" from
Md5.c (the reference C implementation) later
on. ↓ Padding and Length
How we order the input bytes into each word here is important:
[…] a sequence of bytes can be interpreted as a sequence of 32-bit words, where each consecutive group of four bytes is interpreted as a word with the low-order (least significant) byte given first.
Thus we use the first two bytes to compose the "low" 16 bits part of the word, and the third and fourth bytes to compose the "high" 16 bits part.
If we wrap up we get:
step0.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | BEGIN { _ord_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = or(lshift(bytes[i + 3], 8), bytes[i + 2]); lo = or(lshift(bytes[i + 1], 8), bytes[i + 0]); words[nwords++] = or(lshift(hi, 16), lo); } # XXX: debug words and exit: for (i = 0; i < nwords; i++) printf "%4d: %08x\n", i, words[i]; exit; # NOTREACHED } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } |
diff -u base.awk step0.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | --- base.awk 2017-02-20 18:24:03.945445000 +0100 +++ step0.awk 2017-02-20 18:24:03.945454000 +0100 @@ -1,3 +1,7 @@ +BEGIN { + _ord_init(); +} + { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) @@ -17,6 +21,37 @@ } # our md5 implementation -function md5(input) { - # TODO +function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords) { + # convert the input into an array of bytes using ord() on each + # character. + nbytes = split(input, chars, ""); + for (i = 1; i <= nbytes; i++) + bytes[i] = ord(chars[i]); + + # convert the array of bytes into an array of 32-bits words. + # NOTE: words is 0-indexed. + for (i = 1; i <= nbytes; i += 4) { + hi = or(lshift(bytes[i + 3], 8), bytes[i + 2]); + lo = or(lshift(bytes[i + 1], 8), bytes[i + 0]); + words[nwords++] = or(lshift(hi, 16), lo); + } + + # XXX: debug words and exit: + for (i = 0; i < nwords; i++) + printf "%4d: %08x\n", i, words[i]; + exit; + # NOTREACHED +} + +# from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html +function _ord_init( i) +{ + for (i = 0; i < 256; i++) + _ord_[sprintf("%c", i)] = i; +} + +function ord(s) +{ + # only first character is of interest + return _ord_[substr(s, 1, 1)]; } |
We've added the variables used in the md5() function body to the
signature at line 27 and a bit of debug code (lines 41 — 45). Let's make a
quick test with 1234abcd\n:
% echo 1234abcd | xxd -g 1
00000000: 31 32 33 34 61 62 63 64 0a 1234abcd.
This should be familiar (see ascii(7)), In
particular 0a is the ASCII code for \n.
Let's run our script:
% echo 1234abcd | gawk -f step0.awk
0: 34333231
1: 64636261
2: 0000000aAlright! The byte order in each words is as expected: low-order (least significant) byte given first.
Padding Bits and Length
We'll go through "3.1 Step 1. Append Padding Bits" and "3.2 Step 2. Append Length" of the RFC in one go, as I feel like it's easier to visualize and understand both at once. Basically, we need to concatenate
- the input message,
- some padding,
- the input message length.
So that the result looks like this:
[input message][padding][length]The padding is at least a '1' bit, and then as many as '0' bits needed so that the full result can be split into chunks of 512 bits. The trick is to take into account that 64 bits will be "used" by the length.
# Step 1. Append Padding Bits
if (nbytes % 4 == 0) {
# the input size is congruent modulo 32, we need a new word to
# store the first '1' padding bit.
words[nwords++] = 0x80;
} else {
# append a '1' bit in the byte just after the last input byte.
words[nwords - 1] = or(words[nwords - 1], lshift(0x80, (nbytes % 4) * 8));
}
# "fill" the remaining bytes with 0 until we're just shy two words of
# having 16-Word Blocks.
while ((nwords % 16) != 14)
nwords++;The loop at the end may be confusing if you don't remember that in AWK all uninitialized variables (including array values) are 0 by default. As a result, we "only" need to increment the array size to "append zeros" to the array.
The length is represented on 64 bits as two 32-bits words (lower word given first).
# Step 2. Append Length
hi = rshift(nbytes * 8, 32);
lo = (nbytes * 8) - lshift(hi, 32);
words[nwords++] = lo;
words[nwords++] = and(hi, 0xffffffff); # truncate to 32 bitsWe truncate the length if it is bigger than 2^64 as the RFC mandate, just in case you feel like feeding more than 2097152 TiB to AWK.
Let's wrap up again:
step1.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 | BEGIN { _ord_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = or(lshift(bytes[i + 3], 8), bytes[i + 2]); lo = or(lshift(bytes[i + 1], 8), bytes[i + 0]); words[nwords++] = or(lshift(hi, 16), lo); } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. words[nwords++] = 0x80; } else { # append a '1' bit in the byte just after the last input byte. words[nwords - 1] = or(words[nwords - 1], lshift(0x80, (nbytes % 4) * 8)); } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. while ((nwords % 16) != 14) nwords++; # Step 2. Append Length hi = rshift(nbytes * 8, 32); lo = (nbytes * 8) - lshift(hi, 32); words[nwords++] = lo; words[nwords++] = and(hi, 0xffffffff); # truncate to 32 bits # XXX: debug words and exit: for (i = 0; i < nwords; i++) printf "%4d: %08x\n", i, words[i]; exit; # NOTREACHED } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } |
diff -u step0.awk step1.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | --- step0.awk 2017-02-20 18:24:03.945454000 +0100 +++ step1.awk 2017-02-20 18:24:03.945458000 +0100 @@ -36,6 +36,26 @@ words[nwords++] = or(lshift(hi, 16), lo); } + # Step 1. Append Padding Bits + if (nbytes % 4 == 0) { + # the input size is congruent modulo 32, we need a new word to + # store the first '1' padding bit. + words[nwords++] = 0x80; + } else { + # append a '1' bit in the byte just after the last input byte. + words[nwords - 1] = or(words[nwords - 1], lshift(0x80, (nbytes % 4) * 8)); + } + # "fill" the remaining bytes with 0 until we're just shy two words of + # having 16-Word Blocks. + while ((nwords % 16) != 14) + nwords++; + + # Step 2. Append Length + hi = rshift(nbytes * 8, 32); + lo = (nbytes * 8) - lshift(hi, 32); + words[nwords++] = lo; + words[nwords++] = and(hi, 0xffffffff); # truncate to 32 bits + # XXX: debug words and exit: for (i = 0; i < nwords; i++) printf "%4d: %08x\n", i, words[i]; |
Using our previous 1234abcd\n example, the result should look
like:
512 bits
____________________________________________________________________________
/ \
[0x31 0x32 0x33 0x34 0x61 ...][0x80 0x0 ...][0x48 0x0 0x0 0x0 0x0 0x0 0x0 0x0]
\____________________________/\____________/\________________|_______________/
input message padding lower 32-bits higher 32-bits
\________________________________/
lengthLet's test our script:
% echo 1234abcd | gawk -f step1.awk
0: 34333231
1: 64636261
2: 0000800a
3: 00000000
4: 00000000
5: 00000000
6: 00000000
7: 00000000
8: 00000000
9: 00000000
10: 00000000
11: 00000000
12: 00000000
13: 00000000
14: 00000048
15: 00000000
We get as expected 16 32-bits words (i.e. 512 bits) in total,
0x80 right after \n and some zeros to complete the
padding, and finally the length in the two last words.
MD Buffer initialization, Message processing and Output
I will pass quickly through the MD5 rounds and setup, highlighting the challenging parts.
Step 3. is a trivial translation from Md5.c (lines 150 — 155).
# Step 3. Initialize MD Buffer
state[0] = 0x67452301;
state[1] = 0xefcdab89;
state[2] = 0x98badcfe;
state[3] = 0x10325476;
Step 4. was easy too. The main loop and x setup was
adapted directly from the RFC, while the rounds were inspired from
Md5.c. Here having words,
state and x 0-indexed (despite the AWK 1-indexed
arrays tradition) was key to translate almost verbatim the processing loop.
↑ massaging the input
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 | # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. for (i = 0; i < nwords; i += 16) { # Copy block i into x. for (j = 0; j < 16; j++) x[j] = words[i + j]; a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 a = FF(a, b, c, d, x[ 0], S11, 0xd76aa478); d = FF(d, a, b, c, x[ 1], S12, 0xe8c7b756); c = FF(c, d, a, b, x[ 2], S13, 0x242070db); b = FF(b, c, d, a, x[ 3], S14, 0xc1bdceee); a = FF(a, b, c, d, x[ 4], S11, 0xf57c0faf); d = FF(d, a, b, c, x[ 5], S12, 0x4787c62a); c = FF(c, d, a, b, x[ 6], S13, 0xa8304613); b = FF(b, c, d, a, x[ 7], S14, 0xfd469501); a = FF(a, b, c, d, x[ 8], S11, 0x698098d8); d = FF(d, a, b, c, x[ 9], S12, 0x8b44f7af); c = FF(c, d, a, b, x[10], S13, 0xffff5bb1); b = FF(b, c, d, a, x[11], S14, 0x895cd7be); a = FF(a, b, c, d, x[12], S11, 0x6b901122); d = FF(d, a, b, c, x[13], S12, 0xfd987193); c = FF(c, d, a, b, x[14], S13, 0xa679438e); b = FF(b, c, d, a, x[15], S14, 0x49b40821); # Round 2 a = GG(a, b, c, d, x[ 1], S21, 0xf61e2562); d = GG(d, a, b, c, x[ 6], S22, 0xc040b340); c = GG(c, d, a, b, x[11], S23, 0x265e5a51); b = GG(b, c, d, a, x[ 0], S24, 0xe9b6c7aa); a = GG(a, b, c, d, x[ 5], S21, 0xd62f105d); d = GG(d, a, b, c, x[10], S22, 0x2441453); c = GG(c, d, a, b, x[15], S23, 0xd8a1e681); b = GG(b, c, d, a, x[ 4], S24, 0xe7d3fbc8); a = GG(a, b, c, d, x[ 9], S21, 0x21e1cde6); d = GG(d, a, b, c, x[14], S22, 0xc33707d6); c = GG(c, d, a, b, x[ 3], S23, 0xf4d50d87); b = GG(b, c, d, a, x[ 8], S24, 0x455a14ed); a = GG(a, b, c, d, x[13], S21, 0xa9e3e905); d = GG(d, a, b, c, x[ 2], S22, 0xfcefa3f8); c = GG(c, d, a, b, x[ 7], S23, 0x676f02d9); b = GG(b, c, d, a, x[12], S24, 0x8d2a4c8a); # Round 3 a = HH(a, b, c, d, x[ 5], S31, 0xfffa3942); d = HH(d, a, b, c, x[ 8], S32, 0x8771f681); c = HH(c, d, a, b, x[11], S33, 0x6d9d6122); b = HH(b, c, d, a, x[14], S34, 0xfde5380c); a = HH(a, b, c, d, x[ 1], S31, 0xa4beea44); d = HH(d, a, b, c, x[ 4], S32, 0x4bdecfa9); c = HH(c, d, a, b, x[ 7], S33, 0xf6bb4b60); b = HH(b, c, d, a, x[10], S34, 0xbebfbc70); a = HH(a, b, c, d, x[13], S31, 0x289b7ec6); d = HH(d, a, b, c, x[ 0], S32, 0xeaa127fa); c = HH(c, d, a, b, x[ 3], S33, 0xd4ef3085); b = HH(b, c, d, a, x[ 6], S34, 0x4881d05); a = HH(a, b, c, d, x[ 9], S31, 0xd9d4d039); d = HH(d, a, b, c, x[12], S32, 0xe6db99e5); c = HH(c, d, a, b, x[15], S33, 0x1fa27cf8); b = HH(b, c, d, a, x[ 2], S34, 0xc4ac5665); # Round 4 a = II(a, b, c, d, x[ 0], S41, 0xf4292244); d = II(d, a, b, c, x[ 7], S42, 0x432aff97); c = II(c, d, a, b, x[14], S43, 0xab9423a7); b = II(b, c, d, a, x[ 5], S44, 0xfc93a039); a = II(a, b, c, d, x[12], S41, 0x655b59c3); d = II(d, a, b, c, x[ 3], S42, 0x8f0ccc92); c = II(c, d, a, b, x[10], S43, 0xffeff47d); b = II(b, c, d, a, x[ 1], S44, 0x85845dd1); a = II(a, b, c, d, x[ 8], S41, 0x6fa87e4f); d = II(d, a, b, c, x[15], S42, 0xfe2ce6e0); c = II(c, d, a, b, x[ 6], S43, 0xa3014314); b = II(b, c, d, a, x[13], S44, 0x4e0811a1); a = II(a, b, c, d, x[ 4], S41, 0xf7537e82); d = II(d, a, b, c, x[11], S42, 0xbd3af235); c = II(c, d, a, b, x[ 2], S43, 0x2ad7d2bb); b = II(b, c, d, a, x[ 9], S44, 0xeb86d391); state[0] = mod32bits(state[0] + a); state[1] = mod32bits(state[1] + b); state[2] = mod32bits(state[2] + c); state[3] = mod32bits(state[3] + d); } |
We'll need to setup the shift constants (S11, S12,
S13 and so on) and also implement the round functions (namely
FF, GG, HH, and II).
An interesting point is that when state is updated (lines 81 —
84) we have to use "modulo-2^32 addition". As it will be the case
for all additions, we'll write a mod32bits() helper function. If
you remember we already had to implement "32-bits truncation" for the "high
32-bits" part of length:
words[nwords++] = and(hi, 0xffffffff); # truncate to 32 bitsThis will do fine for now:
function mod32bits(x) {
return and(x, 0xffffffff);
}Output
Similarly to the last part of MD5Final(), the 32-bits
state words is "converted" into a digest of 16
bytes. Then, the hexadecimal string representation of the hash is built and
returned.
for (i = j = 0; j < 16; j += 4) {
digest[j + 0] = and(state[i], 0xff);
digest[j + 1] = and(rshift(state[i], 8), 0xff);
digest[j + 2] = and(rshift(state[i], 16), 0xff);
digest[j + 3] = and(rshift(state[i++], 24), 0xff);
}
for (i = 0; i < 16; i++)
ret = sprintf("%s%02x", ret, digest[i]);
return ret;It could be made shorter (and faster) but I've left it in two steps as I find it more readable. The performance penalty should not be significant as this part is O(1), in other words it run in constant time regardless of the input message length.
Round functions
Again, overall easy translation from the reference implementation:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | function F(x, y, z) { return or(and(x, y), and(not(x), z)); } function G(x, y, z) { return or(and(x, z), and(y, not(z))); } function H(x, y, z) { return xor(x, xor(y, z)); } function I(x, y, z) { return xor(y, or(x, not(z))); } function FF(a, b, c, d, x, s, ac) { a = mod32bits(a + F(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function GG(a, b, c, d, x, s, ac) { a = mod32bits(a + G(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function HH(a, b, c, d, x, s, ac) { a = mod32bits(a + H(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function II(a, b, c, d, x, s, ac) { a = mod32bits(a + I(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function ROTATE_LEFT(x, n) { return or(mod32bits(lshift(x, n)), rshift(x, 32 - n)); } function not(x) { return mod32bits(compl(x)); } |
We need to be careful with both lshift() (line 46) and
compl() (line 50) as their return value may be greater than
2^32:
For all of these functions, first the double-precision floating-point value is converted to the widest C unsigned integer type, then the bitwise operation is performed. If the result cannot be represented exactly as a C double, leading nonzero bits are removed one by one until it can be represented exactly. The result is then converted back into a C double. (If you don’t understand this paragraph, don’t worry about it.)
"the widest C unsigned integer type" is likely to be represented on more than
32-bits, and so we're ensuring in both ROTATE_LEFT() and
not() to truncate the result to 32-bits.
Shift constants
Simple and inspired by _ord_init() that we previously adapted:
function _md5_init() {
# MD5 shift constants setup.
S11 = 7; S12 = 12; S13 = 17; S14 = 22;
S21 = 5; S22 = 9; S23 = 14; S24 = 20;
S31 = 4; S32 = 11; S33 = 16; S34 = 23;
S41 = 6; S42 = 10; S43 = 15; S44 = 21;
}
Finally it should work! Here is the final GNU Awk code:
step2.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 | BEGIN { _ord_init(); _md5_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, a, b, c, d, j, x, digest, ret) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = or(lshift(bytes[i + 3], 8), bytes[i + 2]); lo = or(lshift(bytes[i + 1], 8), bytes[i + 0]); words[nwords++] = or(lshift(hi, 16), lo); } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. words[nwords++] = 0x80; } else { # append a '1' bit in the byte just after the last input byte. words[nwords - 1] = or(words[nwords - 1], lshift(0x80, (nbytes % 4) * 8)); } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. while ((nwords % 16) != 14) nwords++; # Step 2. Append Length hi = rshift(nbytes * 8, 32); lo = (nbytes * 8) - lshift(hi, 32); words[nwords++] = lo; words[nwords++] = mod32bits(hi); # truncate to 32 bits # Step 3. Initialize MD Buffer state[0] = 0x67452301; state[1] = 0xefcdab89; state[2] = 0x98badcfe; state[3] = 0x10325476; # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. for (i = 0; i < nwords; i += 16) { # Copy block i into x. for (j = 0; j < 16; j++) x[j] = words[i + j]; a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 a = FF(a, b, c, d, x[ 0], S11, 0xd76aa478); d = FF(d, a, b, c, x[ 1], S12, 0xe8c7b756); c = FF(c, d, a, b, x[ 2], S13, 0x242070db); b = FF(b, c, d, a, x[ 3], S14, 0xc1bdceee); a = FF(a, b, c, d, x[ 4], S11, 0xf57c0faf); d = FF(d, a, b, c, x[ 5], S12, 0x4787c62a); c = FF(c, d, a, b, x[ 6], S13, 0xa8304613); b = FF(b, c, d, a, x[ 7], S14, 0xfd469501); a = FF(a, b, c, d, x[ 8], S11, 0x698098d8); d = FF(d, a, b, c, x[ 9], S12, 0x8b44f7af); c = FF(c, d, a, b, x[10], S13, 0xffff5bb1); b = FF(b, c, d, a, x[11], S14, 0x895cd7be); a = FF(a, b, c, d, x[12], S11, 0x6b901122); d = FF(d, a, b, c, x[13], S12, 0xfd987193); c = FF(c, d, a, b, x[14], S13, 0xa679438e); b = FF(b, c, d, a, x[15], S14, 0x49b40821); # Round 2 a = GG(a, b, c, d, x[ 1], S21, 0xf61e2562); d = GG(d, a, b, c, x[ 6], S22, 0xc040b340); c = GG(c, d, a, b, x[11], S23, 0x265e5a51); b = GG(b, c, d, a, x[ 0], S24, 0xe9b6c7aa); a = GG(a, b, c, d, x[ 5], S21, 0xd62f105d); d = GG(d, a, b, c, x[10], S22, 0x2441453); c = GG(c, d, a, b, x[15], S23, 0xd8a1e681); b = GG(b, c, d, a, x[ 4], S24, 0xe7d3fbc8); a = GG(a, b, c, d, x[ 9], S21, 0x21e1cde6); d = GG(d, a, b, c, x[14], S22, 0xc33707d6); c = GG(c, d, a, b, x[ 3], S23, 0xf4d50d87); b = GG(b, c, d, a, x[ 8], S24, 0x455a14ed); a = GG(a, b, c, d, x[13], S21, 0xa9e3e905); d = GG(d, a, b, c, x[ 2], S22, 0xfcefa3f8); c = GG(c, d, a, b, x[ 7], S23, 0x676f02d9); b = GG(b, c, d, a, x[12], S24, 0x8d2a4c8a); # Round 3 a = HH(a, b, c, d, x[ 5], S31, 0xfffa3942); d = HH(d, a, b, c, x[ 8], S32, 0x8771f681); c = HH(c, d, a, b, x[11], S33, 0x6d9d6122); b = HH(b, c, d, a, x[14], S34, 0xfde5380c); a = HH(a, b, c, d, x[ 1], S31, 0xa4beea44); d = HH(d, a, b, c, x[ 4], S32, 0x4bdecfa9); c = HH(c, d, a, b, x[ 7], S33, 0xf6bb4b60); b = HH(b, c, d, a, x[10], S34, 0xbebfbc70); a = HH(a, b, c, d, x[13], S31, 0x289b7ec6); d = HH(d, a, b, c, x[ 0], S32, 0xeaa127fa); c = HH(c, d, a, b, x[ 3], S33, 0xd4ef3085); b = HH(b, c, d, a, x[ 6], S34, 0x4881d05); a = HH(a, b, c, d, x[ 9], S31, 0xd9d4d039); d = HH(d, a, b, c, x[12], S32, 0xe6db99e5); c = HH(c, d, a, b, x[15], S33, 0x1fa27cf8); b = HH(b, c, d, a, x[ 2], S34, 0xc4ac5665); # Round 4 a = II(a, b, c, d, x[ 0], S41, 0xf4292244); d = II(d, a, b, c, x[ 7], S42, 0x432aff97); c = II(c, d, a, b, x[14], S43, 0xab9423a7); b = II(b, c, d, a, x[ 5], S44, 0xfc93a039); a = II(a, b, c, d, x[12], S41, 0x655b59c3); d = II(d, a, b, c, x[ 3], S42, 0x8f0ccc92); c = II(c, d, a, b, x[10], S43, 0xffeff47d); b = II(b, c, d, a, x[ 1], S44, 0x85845dd1); a = II(a, b, c, d, x[ 8], S41, 0x6fa87e4f); d = II(d, a, b, c, x[15], S42, 0xfe2ce6e0); c = II(c, d, a, b, x[ 6], S43, 0xa3014314); b = II(b, c, d, a, x[13], S44, 0x4e0811a1); a = II(a, b, c, d, x[ 4], S41, 0xf7537e82); d = II(d, a, b, c, x[11], S42, 0xbd3af235); c = II(c, d, a, b, x[ 2], S43, 0x2ad7d2bb); b = II(b, c, d, a, x[ 9], S44, 0xeb86d391); state[0] = mod32bits(state[0] + a); state[1] = mod32bits(state[1] + b); state[2] = mod32bits(state[2] + c); state[3] = mod32bits(state[3] + d); } for (i = j = 0; j < 16; j += 4) { digest[j + 0] = and(state[i], 0xff); digest[j + 1] = and(rshift(state[i], 8), 0xff); digest[j + 2] = and(rshift(state[i], 16), 0xff); digest[j + 3] = and(rshift(state[i++], 24), 0xff); } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); return ret; } function F(x, y, z) { return or(and(x, y), and(not(x), z)); } function G(x, y, z) { return or(and(x, z), and(y, not(z))); } function H(x, y, z) { return xor(x, xor(y, z)); } function I(x, y, z) { return xor(y, or(x, not(z))); } function FF(a, b, c, d, x, s, ac) { a = mod32bits(a + F(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function GG(a, b, c, d, x, s, ac) { a = mod32bits(a + G(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function HH(a, b, c, d, x, s, ac) { a = mod32bits(a + H(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function II(a, b, c, d, x, s, ac) { a = mod32bits(a + I(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function ROTATE_LEFT(x, n) { return or(mod32bits(lshift(x, n)), rshift(x, 32 - n)); } function mod32bits(x) { return and(x, 0xffffffff); } function not(x) { return mod32bits(compl(x)); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } function _md5_init() { # MD5 shift constants setup. S11 = 7; S12 = 12; S13 = 17; S14 = 22; S21 = 5; S22 = 9; S23 = 14; S24 = 20; S31 = 4; S32 = 11; S33 = 16; S34 = 23; S41 = 6; S42 = 10; S43 = 15; S44 = 21; } |
diff -u step1.awk step2.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 | --- step1.awk 2017-06-21 09:43:06.590286000 +0200 +++ step2.awk 2019-10-24 09:35:57.779452000 +0200 @@ -1,5 +1,6 @@ BEGIN { _ord_init(); + _md5_init(); } { @@ -21,7 +22,8 @@ } # our md5 implementation -function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords) { +function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, + a, b, c, d, j, x, digest, ret) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); @@ -54,15 +56,167 @@ hi = rshift(nbytes * 8, 32); lo = (nbytes * 8) - lshift(hi, 32); words[nwords++] = lo; - words[nwords++] = and(hi, 0xffffffff); # truncate to 32 bits + words[nwords++] = mod32bits(hi); # truncate to 32 bits - # XXX: debug words and exit: - for (i = 0; i < nwords; i++) - printf "%4d: %08x\n", i, words[i]; - exit; - # NOTREACHED + # Step 3. Initialize MD Buffer + state[0] = 0x67452301; + state[1] = 0xefcdab89; + state[2] = 0x98badcfe; + state[3] = 0x10325476; + + # Step 4. Process Message in 16-Word Blocks + # Process each 16-word block. + for (i = 0; i < nwords; i += 16) { + # Copy block i into x. + for (j = 0; j < 16; j++) + x[j] = words[i + j]; + a = state[0]; b = state[1]; c = state[2]; d = state[3]; + + # Round 1 + a = FF(a, b, c, d, x[ 0], S11, 0xd76aa478); + d = FF(d, a, b, c, x[ 1], S12, 0xe8c7b756); + c = FF(c, d, a, b, x[ 2], S13, 0x242070db); + b = FF(b, c, d, a, x[ 3], S14, 0xc1bdceee); + a = FF(a, b, c, d, x[ 4], S11, 0xf57c0faf); + d = FF(d, a, b, c, x[ 5], S12, 0x4787c62a); + c = FF(c, d, a, b, x[ 6], S13, 0xa8304613); + b = FF(b, c, d, a, x[ 7], S14, 0xfd469501); + a = FF(a, b, c, d, x[ 8], S11, 0x698098d8); + d = FF(d, a, b, c, x[ 9], S12, 0x8b44f7af); + c = FF(c, d, a, b, x[10], S13, 0xffff5bb1); + b = FF(b, c, d, a, x[11], S14, 0x895cd7be); + a = FF(a, b, c, d, x[12], S11, 0x6b901122); + d = FF(d, a, b, c, x[13], S12, 0xfd987193); + c = FF(c, d, a, b, x[14], S13, 0xa679438e); + b = FF(b, c, d, a, x[15], S14, 0x49b40821); + + # Round 2 + a = GG(a, b, c, d, x[ 1], S21, 0xf61e2562); + d = GG(d, a, b, c, x[ 6], S22, 0xc040b340); + c = GG(c, d, a, b, x[11], S23, 0x265e5a51); + b = GG(b, c, d, a, x[ 0], S24, 0xe9b6c7aa); + a = GG(a, b, c, d, x[ 5], S21, 0xd62f105d); + d = GG(d, a, b, c, x[10], S22, 0x2441453); + c = GG(c, d, a, b, x[15], S23, 0xd8a1e681); + b = GG(b, c, d, a, x[ 4], S24, 0xe7d3fbc8); + a = GG(a, b, c, d, x[ 9], S21, 0x21e1cde6); + d = GG(d, a, b, c, x[14], S22, 0xc33707d6); + c = GG(c, d, a, b, x[ 3], S23, 0xf4d50d87); + b = GG(b, c, d, a, x[ 8], S24, 0x455a14ed); + a = GG(a, b, c, d, x[13], S21, 0xa9e3e905); + d = GG(d, a, b, c, x[ 2], S22, 0xfcefa3f8); + c = GG(c, d, a, b, x[ 7], S23, 0x676f02d9); + b = GG(b, c, d, a, x[12], S24, 0x8d2a4c8a); + + # Round 3 + a = HH(a, b, c, d, x[ 5], S31, 0xfffa3942); + d = HH(d, a, b, c, x[ 8], S32, 0x8771f681); + c = HH(c, d, a, b, x[11], S33, 0x6d9d6122); + b = HH(b, c, d, a, x[14], S34, 0xfde5380c); + a = HH(a, b, c, d, x[ 1], S31, 0xa4beea44); + d = HH(d, a, b, c, x[ 4], S32, 0x4bdecfa9); + c = HH(c, d, a, b, x[ 7], S33, 0xf6bb4b60); + b = HH(b, c, d, a, x[10], S34, 0xbebfbc70); + a = HH(a, b, c, d, x[13], S31, 0x289b7ec6); + d = HH(d, a, b, c, x[ 0], S32, 0xeaa127fa); + c = HH(c, d, a, b, x[ 3], S33, 0xd4ef3085); + b = HH(b, c, d, a, x[ 6], S34, 0x4881d05); + a = HH(a, b, c, d, x[ 9], S31, 0xd9d4d039); + d = HH(d, a, b, c, x[12], S32, 0xe6db99e5); + c = HH(c, d, a, b, x[15], S33, 0x1fa27cf8); + b = HH(b, c, d, a, x[ 2], S34, 0xc4ac5665); + + # Round 4 + a = II(a, b, c, d, x[ 0], S41, 0xf4292244); + d = II(d, a, b, c, x[ 7], S42, 0x432aff97); + c = II(c, d, a, b, x[14], S43, 0xab9423a7); + b = II(b, c, d, a, x[ 5], S44, 0xfc93a039); + a = II(a, b, c, d, x[12], S41, 0x655b59c3); + d = II(d, a, b, c, x[ 3], S42, 0x8f0ccc92); + c = II(c, d, a, b, x[10], S43, 0xffeff47d); + b = II(b, c, d, a, x[ 1], S44, 0x85845dd1); + a = II(a, b, c, d, x[ 8], S41, 0x6fa87e4f); + d = II(d, a, b, c, x[15], S42, 0xfe2ce6e0); + c = II(c, d, a, b, x[ 6], S43, 0xa3014314); + b = II(b, c, d, a, x[13], S44, 0x4e0811a1); + a = II(a, b, c, d, x[ 4], S41, 0xf7537e82); + d = II(d, a, b, c, x[11], S42, 0xbd3af235); + c = II(c, d, a, b, x[ 2], S43, 0x2ad7d2bb); + b = II(b, c, d, a, x[ 9], S44, 0xeb86d391); + + state[0] = mod32bits(state[0] + a); + state[1] = mod32bits(state[1] + b); + state[2] = mod32bits(state[2] + c); + state[3] = mod32bits(state[3] + d); + } + + for (i = j = 0; j < 16; j += 4) { + digest[j + 0] = and(state[i], 0xff); + digest[j + 1] = and(rshift(state[i], 8), 0xff); + digest[j + 2] = and(rshift(state[i], 16), 0xff); + digest[j + 3] = and(rshift(state[i++], 24), 0xff); + } + for (i = 0; i < 16; i++) + ret = sprintf("%s%02x", ret, digest[i]); + return ret; } +function F(x, y, z) { + return or(and(x, y), and(not(x), z)); +} + +function G(x, y, z) { + return or(and(x, z), and(y, not(z))); +} + +function H(x, y, z) { + return xor(x, xor(y, z)); +} + +function I(x, y, z) { + return xor(y, or(x, not(z))); +} + +function FF(a, b, c, d, x, s, ac) { + a = mod32bits(a + F(b, c, d) + x + ac); + a = ROTATE_LEFT(a, s); + a = mod32bits(a + b); + return a; +} + +function GG(a, b, c, d, x, s, ac) { + a = mod32bits(a + G(b, c, d) + x + ac); + a = ROTATE_LEFT(a, s); + a = mod32bits(a + b); + return a; +} + +function HH(a, b, c, d, x, s, ac) { + a = mod32bits(a + H(b, c, d) + x + ac); + a = ROTATE_LEFT(a, s); + a = mod32bits(a + b); + return a; +} + +function II(a, b, c, d, x, s, ac) { + a = mod32bits(a + I(b, c, d) + x + ac); + a = ROTATE_LEFT(a, s); + a = mod32bits(a + b); + return a; +} + +function ROTATE_LEFT(x, n) { + return or(mod32bits(lshift(x, n)), rshift(x, 32 - n)); +} + +function mod32bits(x) { + return and(x, 0xffffffff); +} + +function not(x) { + return mod32bits(compl(x)); +} + # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { @@ -74,4 +228,12 @@ { # only first character is of interest return _ord_[substr(s, 1, 1)]; +} + +function _md5_init() { + # MD5 shift constants setup. + S11 = 7; S12 = 12; S13 = 17; S14 = 22; + S21 = 5; S22 = 9; S23 = 14; S24 = 20; + S31 = 4; S32 = 11; S33 = 16; S34 = 23; + S41 = 6; S42 = 10; S43 = 15; S44 = 21; } |
Now, we need a bunch of ASCII files for testing. Arbitrarily, I'll use the SQLite sources files (i.e. files from the src/ directory) because it's enough data without being too much (about 6.5MB for 200k sloc).
We start by computing the MD5 sum for each file using openssl md5
(because we mimic its output):
% time openssl md5 sqlite-src-3160200/src/* | tee /tmp/openssl.md5.out
MD5(sqlite-src-3160200/src/alter.c)= 7aa093f1a5ec92bf94eef2e068aa05da
MD5(sqlite-src-3160200/src/analyze.c)= 9126f817e68ac2a625f816874f6f15e8
MD5(sqlite-src-3160200/src/attach.c)= a945102cc7281d9f01b812be96f24123
...
MD5(sqlite-src-3160200/src/whereexpr.c)= 4af42e1cdcb59e98c9ca916f7fb0bb28
MD5(sqlite-src-3160200/src/whereInt.h)= cb8d28f5101b56b4ebcb5e02077e99b9
openssl md5 sqlite-src-3160200/src/* 0.01s user 0.00s system 71% cpu 0.017 total
tee /tmp/openssl.md5.out 0.00s user 0.00s system 0% cpu 0.018 total
% █
Let's do the same using our script, and finally diff the two
outputs to ensure that our implementation compute the hash correctly:
% time gawk -f step2.awk sqlite-src-3160200/src/* | tee /tmp/step2.out
MD5(sqlite-src-3160200/src/alter.c)= 7aa093f1a5ec92bf94eef2e068aa05da
MD5(sqlite-src-3160200/src/analyze.c)= 9126f817e68ac2a625f816874f6f15e8
MD5(sqlite-src-3160200/src/attach.c)= a945102cc7281d9f01b812be96f24123
...
MD5(sqlite-src-3160200/src/whereexpr.c)= 4af42e1cdcb59e98c9ca916f7fb0bb28
MD5(sqlite-src-3160200/src/whereInt.h)= cb8d28f5101b56b4ebcb5e02077e99b9
gawk -f step2.awk sqlite-src-3160200/src/* 15.85s user 0.13s system 99% cpu 15.985 total
tee /tmp/step2.out 0.00s user 0.00s system 0% cpu 15.984 total
% diff -u /tmp/step2.out /tmp/openssl.md5.out
% █Victory! Our implementation seems correct and take about 16s (on my machine) to compute all the MD5 hashes. The timings show that our implementation is roughly three order of magnitude slower than openssl. It is actually even worst as we can see that the openssl command was not using the CPU about one third of the time (probably waiting on I/O).
Now we're not trying to race the openssl command of course, but it gives a good idea of how impractical our implementation is for use beyond a coding challenge. Furthermore, our implementation is going to be only slower from now on.
From GNU Awk to AWK
In order to focus on our initial problem of implementing the MD5 algorithm, we've used two GNU Awk features unavailable in AWK:
-
hexadecimal numbers literal (e.g.,
0xff) -
bitwise functions:
or,and,xor,compl,lshift, andrshift.
Now that we've successfully wrote the MD5 part, let's "port" our implementation to AWK.
hexadecimal numbers and wrappers
Replacing hexadecimal numbers is going to be trivial, just a pinch of Perl one-liner and some handmade alignment fixes:
% perl -pe 's/(.*)(0x[0-9a-fA-F]+)(.*)/$1.hex($2).$3." # ".$2/e' step2.awkWe'll also "wrap" the bitwise functions that we intent to re-implement, so that their names don't clash with GNU Awk built-in functions. Now the script looks like this:
step3.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 | BEGIN { _ord_init(); _md5_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, a, b, c, d, j, x, digest, ret) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = bw_or(bw_lshift(bytes[i + 3], 8), bytes[i + 2]); lo = bw_or(bw_lshift(bytes[i + 1], 8), bytes[i + 0]); words[nwords++] = bw_or(bw_lshift(hi, 16), lo); } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. words[nwords++] = 128; # 0x80 } else { # append a '1' bit in the byte just after the last input byte. words[nwords - 1] = bw_or(words[nwords - 1], bw_lshift(128, (nbytes % 4) * 8)); # 0x80 } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. while ((nwords % 16) != 14) nwords++; # Step 2. Append Length hi = bw_rshift(nbytes * 8, 32); lo = (nbytes * 8) - bw_lshift(hi, 32); words[nwords++] = lo; words[nwords++] = mod32bits(hi); # truncate to 32 bits # Step 3. Initialize MD Buffer state[0] = 1732584193; # 0x67452301 state[1] = 4023233417; # 0xefcdab89 state[2] = 2562383102; # 0x98badcfe state[3] = 271733878; # 0x10325476 # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. for (i = 0; i < nwords; i += 16) { # Copy block i into x. for (j = 0; j < 16; j++) x[j] = words[i + j]; a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 a = FF(a, b, c, d, x[ 0], S11, 3614090360); # 0xd76aa478 d = FF(d, a, b, c, x[ 1], S12, 3905402710); # 0xe8c7b756 c = FF(c, d, a, b, x[ 2], S13, 606105819); # 0x242070db b = FF(b, c, d, a, x[ 3], S14, 3250441966); # 0xc1bdceee a = FF(a, b, c, d, x[ 4], S11, 4118548399); # 0xf57c0faf d = FF(d, a, b, c, x[ 5], S12, 1200080426); # 0x4787c62a c = FF(c, d, a, b, x[ 6], S13, 2821735955); # 0xa8304613 b = FF(b, c, d, a, x[ 7], S14, 4249261313); # 0xfd469501 a = FF(a, b, c, d, x[ 8], S11, 1770035416); # 0x698098d8 d = FF(d, a, b, c, x[ 9], S12, 2336552879); # 0x8b44f7af c = FF(c, d, a, b, x[10], S13, 4294925233); # 0xffff5bb1 b = FF(b, c, d, a, x[11], S14, 2304563134); # 0x895cd7be a = FF(a, b, c, d, x[12], S11, 1804603682); # 0x6b901122 d = FF(d, a, b, c, x[13], S12, 4254626195); # 0xfd987193 c = FF(c, d, a, b, x[14], S13, 2792965006); # 0xa679438e b = FF(b, c, d, a, x[15], S14, 1236535329); # 0x49b40821 # Round 2 a = GG(a, b, c, d, x[ 1], S21, 4129170786); # 0xf61e2562 d = GG(d, a, b, c, x[ 6], S22, 3225465664); # 0xc040b340 c = GG(c, d, a, b, x[11], S23, 643717713); # 0x265e5a51 b = GG(b, c, d, a, x[ 0], S24, 3921069994); # 0xe9b6c7aa a = GG(a, b, c, d, x[ 5], S21, 3593408605); # 0xd62f105d d = GG(d, a, b, c, x[10], S22, 38016083); # 0x2441453 c = GG(c, d, a, b, x[15], S23, 3634488961); # 0xd8a1e681 b = GG(b, c, d, a, x[ 4], S24, 3889429448); # 0xe7d3fbc8 a = GG(a, b, c, d, x[ 9], S21, 568446438); # 0x21e1cde6 d = GG(d, a, b, c, x[14], S22, 3275163606); # 0xc33707d6 c = GG(c, d, a, b, x[ 3], S23, 4107603335); # 0xf4d50d87 b = GG(b, c, d, a, x[ 8], S24, 1163531501); # 0x455a14ed a = GG(a, b, c, d, x[13], S21, 2850285829); # 0xa9e3e905 d = GG(d, a, b, c, x[ 2], S22, 4243563512); # 0xfcefa3f8 c = GG(c, d, a, b, x[ 7], S23, 1735328473); # 0x676f02d9 b = GG(b, c, d, a, x[12], S24, 2368359562); # 0x8d2a4c8a # Round 3 a = HH(a, b, c, d, x[ 5], S31, 4294588738); # 0xfffa3942 d = HH(d, a, b, c, x[ 8], S32, 2272392833); # 0x8771f681 c = HH(c, d, a, b, x[11], S33, 1839030562); # 0x6d9d6122 b = HH(b, c, d, a, x[14], S34, 4259657740); # 0xfde5380c a = HH(a, b, c, d, x[ 1], S31, 2763975236); # 0xa4beea44 d = HH(d, a, b, c, x[ 4], S32, 1272893353); # 0x4bdecfa9 c = HH(c, d, a, b, x[ 7], S33, 4139469664); # 0xf6bb4b60 b = HH(b, c, d, a, x[10], S34, 3200236656); # 0xbebfbc70 a = HH(a, b, c, d, x[13], S31, 681279174); # 0x289b7ec6 d = HH(d, a, b, c, x[ 0], S32, 3936430074); # 0xeaa127fa c = HH(c, d, a, b, x[ 3], S33, 3572445317); # 0xd4ef3085 b = HH(b, c, d, a, x[ 6], S34, 76029189); # 0x4881d05 a = HH(a, b, c, d, x[ 9], S31, 3654602809); # 0xd9d4d039 d = HH(d, a, b, c, x[12], S32, 3873151461); # 0xe6db99e5 c = HH(c, d, a, b, x[15], S33, 530742520); # 0x1fa27cf8 b = HH(b, c, d, a, x[ 2], S34, 3299628645); # 0xc4ac5665 # Round 4 a = II(a, b, c, d, x[ 0], S41, 4096336452); # 0xf4292244 d = II(d, a, b, c, x[ 7], S42, 1126891415); # 0x432aff97 c = II(c, d, a, b, x[14], S43, 2878612391); # 0xab9423a7 b = II(b, c, d, a, x[ 5], S44, 4237533241); # 0xfc93a039 a = II(a, b, c, d, x[12], S41, 1700485571); # 0x655b59c3 d = II(d, a, b, c, x[ 3], S42, 2399980690); # 0x8f0ccc92 c = II(c, d, a, b, x[10], S43, 4293915773); # 0xffeff47d b = II(b, c, d, a, x[ 1], S44, 2240044497); # 0x85845dd1 a = II(a, b, c, d, x[ 8], S41, 1873313359); # 0x6fa87e4f d = II(d, a, b, c, x[15], S42, 4264355552); # 0xfe2ce6e0 c = II(c, d, a, b, x[ 6], S43, 2734768916); # 0xa3014314 b = II(b, c, d, a, x[13], S44, 1309151649); # 0x4e0811a1 a = II(a, b, c, d, x[ 4], S41, 4149444226); # 0xf7537e82 d = II(d, a, b, c, x[11], S42, 3174756917); # 0xbd3af235 c = II(c, d, a, b, x[ 2], S43, 718787259); # 0x2ad7d2bb b = II(b, c, d, a, x[ 9], S44, 3951481745); # 0xeb86d391 state[0] = mod32bits(state[0] + a); state[1] = mod32bits(state[1] + b); state[2] = mod32bits(state[2] + c); state[3] = mod32bits(state[3] + d); } for (i = j = 0; j < 16; j += 4) { digest[j + 0] = bw_and(state[i], 255); # 0xff digest[j + 1] = bw_and(bw_rshift(state[i], 8), 255); # 0xff digest[j + 2] = bw_and(bw_rshift(state[i], 16), 255); # 0xff digest[j + 3] = bw_and(bw_rshift(state[i++], 24), 255); # 0xff } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); return ret; } function F(x, y, z) { return bw_or(bw_and(x, y), bw_and(bw_not(x), z)); } function G(x, y, z) { return bw_or(bw_and(x, z), bw_and(y, bw_not(z))); } function H(x, y, z) { return bw_xor(x, bw_xor(y, z)); } function I(x, y, z) { return bw_xor(y, bw_or(x, bw_not(z))); } function FF(a, b, c, d, x, s, ac) { a = mod32bits(a + F(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function GG(a, b, c, d, x, s, ac) { a = mod32bits(a + G(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function HH(a, b, c, d, x, s, ac) { a = mod32bits(a + H(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function II(a, b, c, d, x, s, ac) { a = mod32bits(a + I(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function ROTATE_LEFT(x, n) { return bw_or(mod32bits(bw_lshift(x, n)), bw_rshift(x, 32 - n)); } function mod32bits(x) { return bw_and(x, 4294967295); # 0xffffffff } function bw_not(x) { return mod32bits(compl(x)); } function bw_lshift(x, n) { return lshift(x, n); } function bw_rshift(x, n) { return rshift(x, n); } function bw_and(x, y) { return and(x, y); } function bw_or(x, y) { return or(x, y); } function bw_xor(x, y) { return xor(x, y); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } function _md5_init() { # MD5 shift constants setup. S11 = 7; S12 = 12; S13 = 17; S14 = 22; S21 = 5; S22 = 9; S23 = 14; S24 = 20; S31 = 4; S32 = 11; S33 = 16; S34 = 23; S41 = 6; S42 = 10; S43 = 15; S44 = 21; } |
diff -u step2.awk step3.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 | --- step2.awk 2019-10-24 09:35:57.779452000 +0200 +++ step3.awk 2017-06-21 09:43:06.599989000 +0200 @@ -33,19 +33,19 @@ # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { - hi = or(lshift(bytes[i + 3], 8), bytes[i + 2]); - lo = or(lshift(bytes[i + 1], 8), bytes[i + 0]); - words[nwords++] = or(lshift(hi, 16), lo); + hi = bw_or(bw_lshift(bytes[i + 3], 8), bytes[i + 2]); + lo = bw_or(bw_lshift(bytes[i + 1], 8), bytes[i + 0]); + words[nwords++] = bw_or(bw_lshift(hi, 16), lo); } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. - words[nwords++] = 0x80; + words[nwords++] = 128; # 0x80 } else { # append a '1' bit in the byte just after the last input byte. - words[nwords - 1] = or(words[nwords - 1], lshift(0x80, (nbytes % 4) * 8)); + words[nwords - 1] = bw_or(words[nwords - 1], bw_lshift(128, (nbytes % 4) * 8)); # 0x80 } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. @@ -53,16 +53,16 @@ nwords++; # Step 2. Append Length - hi = rshift(nbytes * 8, 32); - lo = (nbytes * 8) - lshift(hi, 32); + hi = bw_rshift(nbytes * 8, 32); + lo = (nbytes * 8) - bw_lshift(hi, 32); words[nwords++] = lo; words[nwords++] = mod32bits(hi); # truncate to 32 bits # Step 3. Initialize MD Buffer - state[0] = 0x67452301; - state[1] = 0xefcdab89; - state[2] = 0x98badcfe; - state[3] = 0x10325476; + state[0] = 1732584193; # 0x67452301 + state[1] = 4023233417; # 0xefcdab89 + state[2] = 2562383102; # 0x98badcfe + state[3] = 271733878; # 0x10325476 # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. @@ -73,76 +73,76 @@ a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 - a = FF(a, b, c, d, x[ 0], S11, 0xd76aa478); - d = FF(d, a, b, c, x[ 1], S12, 0xe8c7b756); - c = FF(c, d, a, b, x[ 2], S13, 0x242070db); - b = FF(b, c, d, a, x[ 3], S14, 0xc1bdceee); - a = FF(a, b, c, d, x[ 4], S11, 0xf57c0faf); - d = FF(d, a, b, c, x[ 5], S12, 0x4787c62a); - c = FF(c, d, a, b, x[ 6], S13, 0xa8304613); - b = FF(b, c, d, a, x[ 7], S14, 0xfd469501); - a = FF(a, b, c, d, x[ 8], S11, 0x698098d8); - d = FF(d, a, b, c, x[ 9], S12, 0x8b44f7af); - c = FF(c, d, a, b, x[10], S13, 0xffff5bb1); - b = FF(b, c, d, a, x[11], S14, 0x895cd7be); - a = FF(a, b, c, d, x[12], S11, 0x6b901122); - d = FF(d, a, b, c, x[13], S12, 0xfd987193); - c = FF(c, d, a, b, x[14], S13, 0xa679438e); - b = FF(b, c, d, a, x[15], S14, 0x49b40821); + a = FF(a, b, c, d, x[ 0], S11, 3614090360); # 0xd76aa478 + d = FF(d, a, b, c, x[ 1], S12, 3905402710); # 0xe8c7b756 + c = FF(c, d, a, b, x[ 2], S13, 606105819); # 0x242070db + b = FF(b, c, d, a, x[ 3], S14, 3250441966); # 0xc1bdceee + a = FF(a, b, c, d, x[ 4], S11, 4118548399); # 0xf57c0faf + d = FF(d, a, b, c, x[ 5], S12, 1200080426); # 0x4787c62a + c = FF(c, d, a, b, x[ 6], S13, 2821735955); # 0xa8304613 + b = FF(b, c, d, a, x[ 7], S14, 4249261313); # 0xfd469501 + a = FF(a, b, c, d, x[ 8], S11, 1770035416); # 0x698098d8 + d = FF(d, a, b, c, x[ 9], S12, 2336552879); # 0x8b44f7af + c = FF(c, d, a, b, x[10], S13, 4294925233); # 0xffff5bb1 + b = FF(b, c, d, a, x[11], S14, 2304563134); # 0x895cd7be + a = FF(a, b, c, d, x[12], S11, 1804603682); # 0x6b901122 + d = FF(d, a, b, c, x[13], S12, 4254626195); # 0xfd987193 + c = FF(c, d, a, b, x[14], S13, 2792965006); # 0xa679438e + b = FF(b, c, d, a, x[15], S14, 1236535329); # 0x49b40821 # Round 2 - a = GG(a, b, c, d, x[ 1], S21, 0xf61e2562); - d = GG(d, a, b, c, x[ 6], S22, 0xc040b340); - c = GG(c, d, a, b, x[11], S23, 0x265e5a51); - b = GG(b, c, d, a, x[ 0], S24, 0xe9b6c7aa); - a = GG(a, b, c, d, x[ 5], S21, 0xd62f105d); - d = GG(d, a, b, c, x[10], S22, 0x2441453); - c = GG(c, d, a, b, x[15], S23, 0xd8a1e681); - b = GG(b, c, d, a, x[ 4], S24, 0xe7d3fbc8); - a = GG(a, b, c, d, x[ 9], S21, 0x21e1cde6); - d = GG(d, a, b, c, x[14], S22, 0xc33707d6); - c = GG(c, d, a, b, x[ 3], S23, 0xf4d50d87); - b = GG(b, c, d, a, x[ 8], S24, 0x455a14ed); - a = GG(a, b, c, d, x[13], S21, 0xa9e3e905); - d = GG(d, a, b, c, x[ 2], S22, 0xfcefa3f8); - c = GG(c, d, a, b, x[ 7], S23, 0x676f02d9); - b = GG(b, c, d, a, x[12], S24, 0x8d2a4c8a); + a = GG(a, b, c, d, x[ 1], S21, 4129170786); # 0xf61e2562 + d = GG(d, a, b, c, x[ 6], S22, 3225465664); # 0xc040b340 + c = GG(c, d, a, b, x[11], S23, 643717713); # 0x265e5a51 + b = GG(b, c, d, a, x[ 0], S24, 3921069994); # 0xe9b6c7aa + a = GG(a, b, c, d, x[ 5], S21, 3593408605); # 0xd62f105d + d = GG(d, a, b, c, x[10], S22, 38016083); # 0x2441453 + c = GG(c, d, a, b, x[15], S23, 3634488961); # 0xd8a1e681 + b = GG(b, c, d, a, x[ 4], S24, 3889429448); # 0xe7d3fbc8 + a = GG(a, b, c, d, x[ 9], S21, 568446438); # 0x21e1cde6 + d = GG(d, a, b, c, x[14], S22, 3275163606); # 0xc33707d6 + c = GG(c, d, a, b, x[ 3], S23, 4107603335); # 0xf4d50d87 + b = GG(b, c, d, a, x[ 8], S24, 1163531501); # 0x455a14ed + a = GG(a, b, c, d, x[13], S21, 2850285829); # 0xa9e3e905 + d = GG(d, a, b, c, x[ 2], S22, 4243563512); # 0xfcefa3f8 + c = GG(c, d, a, b, x[ 7], S23, 1735328473); # 0x676f02d9 + b = GG(b, c, d, a, x[12], S24, 2368359562); # 0x8d2a4c8a # Round 3 - a = HH(a, b, c, d, x[ 5], S31, 0xfffa3942); - d = HH(d, a, b, c, x[ 8], S32, 0x8771f681); - c = HH(c, d, a, b, x[11], S33, 0x6d9d6122); - b = HH(b, c, d, a, x[14], S34, 0xfde5380c); - a = HH(a, b, c, d, x[ 1], S31, 0xa4beea44); - d = HH(d, a, b, c, x[ 4], S32, 0x4bdecfa9); - c = HH(c, d, a, b, x[ 7], S33, 0xf6bb4b60); - b = HH(b, c, d, a, x[10], S34, 0xbebfbc70); - a = HH(a, b, c, d, x[13], S31, 0x289b7ec6); - d = HH(d, a, b, c, x[ 0], S32, 0xeaa127fa); - c = HH(c, d, a, b, x[ 3], S33, 0xd4ef3085); - b = HH(b, c, d, a, x[ 6], S34, 0x4881d05); - a = HH(a, b, c, d, x[ 9], S31, 0xd9d4d039); - d = HH(d, a, b, c, x[12], S32, 0xe6db99e5); - c = HH(c, d, a, b, x[15], S33, 0x1fa27cf8); - b = HH(b, c, d, a, x[ 2], S34, 0xc4ac5665); + a = HH(a, b, c, d, x[ 5], S31, 4294588738); # 0xfffa3942 + d = HH(d, a, b, c, x[ 8], S32, 2272392833); # 0x8771f681 + c = HH(c, d, a, b, x[11], S33, 1839030562); # 0x6d9d6122 + b = HH(b, c, d, a, x[14], S34, 4259657740); # 0xfde5380c + a = HH(a, b, c, d, x[ 1], S31, 2763975236); # 0xa4beea44 + d = HH(d, a, b, c, x[ 4], S32, 1272893353); # 0x4bdecfa9 + c = HH(c, d, a, b, x[ 7], S33, 4139469664); # 0xf6bb4b60 + b = HH(b, c, d, a, x[10], S34, 3200236656); # 0xbebfbc70 + a = HH(a, b, c, d, x[13], S31, 681279174); # 0x289b7ec6 + d = HH(d, a, b, c, x[ 0], S32, 3936430074); # 0xeaa127fa + c = HH(c, d, a, b, x[ 3], S33, 3572445317); # 0xd4ef3085 + b = HH(b, c, d, a, x[ 6], S34, 76029189); # 0x4881d05 + a = HH(a, b, c, d, x[ 9], S31, 3654602809); # 0xd9d4d039 + d = HH(d, a, b, c, x[12], S32, 3873151461); # 0xe6db99e5 + c = HH(c, d, a, b, x[15], S33, 530742520); # 0x1fa27cf8 + b = HH(b, c, d, a, x[ 2], S34, 3299628645); # 0xc4ac5665 # Round 4 - a = II(a, b, c, d, x[ 0], S41, 0xf4292244); - d = II(d, a, b, c, x[ 7], S42, 0x432aff97); - c = II(c, d, a, b, x[14], S43, 0xab9423a7); - b = II(b, c, d, a, x[ 5], S44, 0xfc93a039); - a = II(a, b, c, d, x[12], S41, 0x655b59c3); - d = II(d, a, b, c, x[ 3], S42, 0x8f0ccc92); - c = II(c, d, a, b, x[10], S43, 0xffeff47d); - b = II(b, c, d, a, x[ 1], S44, 0x85845dd1); - a = II(a, b, c, d, x[ 8], S41, 0x6fa87e4f); - d = II(d, a, b, c, x[15], S42, 0xfe2ce6e0); - c = II(c, d, a, b, x[ 6], S43, 0xa3014314); - b = II(b, c, d, a, x[13], S44, 0x4e0811a1); - a = II(a, b, c, d, x[ 4], S41, 0xf7537e82); - d = II(d, a, b, c, x[11], S42, 0xbd3af235); - c = II(c, d, a, b, x[ 2], S43, 0x2ad7d2bb); - b = II(b, c, d, a, x[ 9], S44, 0xeb86d391); + a = II(a, b, c, d, x[ 0], S41, 4096336452); # 0xf4292244 + d = II(d, a, b, c, x[ 7], S42, 1126891415); # 0x432aff97 + c = II(c, d, a, b, x[14], S43, 2878612391); # 0xab9423a7 + b = II(b, c, d, a, x[ 5], S44, 4237533241); # 0xfc93a039 + a = II(a, b, c, d, x[12], S41, 1700485571); # 0x655b59c3 + d = II(d, a, b, c, x[ 3], S42, 2399980690); # 0x8f0ccc92 + c = II(c, d, a, b, x[10], S43, 4293915773); # 0xffeff47d + b = II(b, c, d, a, x[ 1], S44, 2240044497); # 0x85845dd1 + a = II(a, b, c, d, x[ 8], S41, 1873313359); # 0x6fa87e4f + d = II(d, a, b, c, x[15], S42, 4264355552); # 0xfe2ce6e0 + c = II(c, d, a, b, x[ 6], S43, 2734768916); # 0xa3014314 + b = II(b, c, d, a, x[13], S44, 1309151649); # 0x4e0811a1 + a = II(a, b, c, d, x[ 4], S41, 4149444226); # 0xf7537e82 + d = II(d, a, b, c, x[11], S42, 3174756917); # 0xbd3af235 + c = II(c, d, a, b, x[ 2], S43, 718787259); # 0x2ad7d2bb + b = II(b, c, d, a, x[ 9], S44, 3951481745); # 0xeb86d391 state[0] = mod32bits(state[0] + a); state[1] = mod32bits(state[1] + b); @@ -151,10 +151,10 @@ } for (i = j = 0; j < 16; j += 4) { - digest[j + 0] = and(state[i], 0xff); - digest[j + 1] = and(rshift(state[i], 8), 0xff); - digest[j + 2] = and(rshift(state[i], 16), 0xff); - digest[j + 3] = and(rshift(state[i++], 24), 0xff); + digest[j + 0] = bw_and(state[i], 255); # 0xff + digest[j + 1] = bw_and(bw_rshift(state[i], 8), 255); # 0xff + digest[j + 2] = bw_and(bw_rshift(state[i], 16), 255); # 0xff + digest[j + 3] = bw_and(bw_rshift(state[i++], 24), 255); # 0xff } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); @@ -162,19 +162,19 @@ } function F(x, y, z) { - return or(and(x, y), and(not(x), z)); + return bw_or(bw_and(x, y), bw_and(bw_not(x), z)); } function G(x, y, z) { - return or(and(x, z), and(y, not(z))); + return bw_or(bw_and(x, z), bw_and(y, bw_not(z))); } function H(x, y, z) { - return xor(x, xor(y, z)); + return bw_xor(x, bw_xor(y, z)); } function I(x, y, z) { - return xor(y, or(x, not(z))); + return bw_xor(y, bw_or(x, bw_not(z))); } function FF(a, b, c, d, x, s, ac) { @@ -206,15 +206,35 @@ } function ROTATE_LEFT(x, n) { - return or(mod32bits(lshift(x, n)), rshift(x, 32 - n)); + return bw_or(mod32bits(bw_lshift(x, n)), bw_rshift(x, 32 - n)); } function mod32bits(x) { - return and(x, 0xffffffff); + return bw_and(x, 4294967295); # 0xffffffff } -function not(x) { +function bw_not(x) { return mod32bits(compl(x)); +} + +function bw_lshift(x, n) { + return lshift(x, n); +} + +function bw_rshift(x, n) { + return rshift(x, n); +} + +function bw_and(x, y) { + return and(x, y); +} + +function bw_or(x, y) { + return or(x, y); +} + +function bw_xor(x, y) { + return xor(x, y); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html |
We'll assume that the hexadecimal change did not impact performances, but "wrapping" the bitwise functions is expected to incur an overhead as they are intensively used by the MD5 rounds:
% time gawk -f step3.awk sqlite-src-3160200/src/* | tee /tmp/step3.out
...
gawk -f step3.awk sqlite-src-3160200/src/* 24.73s user 0.23s system 99% cpu 24.962 total
tee /tmp/step3.out 0.00s user 0.00s system 0% cpu 24.961 totalIf we compare to the step2.awk timing (about 16s), this version is ~56% slower (!) Hang on though, as I'm sure we can do worse ;)
lshift & rshift
We need to implement the bitwise functions based on what AWK has to offer.
Because we feel like we have a hint, let's start with lshift and
rshift.
A classic "bit trick" in C (and others languages) to perform multiplication
and division on unsigned integer by a power of two is to use logical
left shift and logical right shift (respectively). Here we can do the
opposite, i.e. using multiplication and division to implement our
bw_lshift and bw_rshift functions:
step4.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 | BEGIN { _ord_init(); _md5_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, a, b, c, d, j, x, digest, ret) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = bw_or(bw_lshift(bytes[i + 3], 8), bytes[i + 2]); lo = bw_or(bw_lshift(bytes[i + 1], 8), bytes[i + 0]); words[nwords++] = bw_or(bw_lshift(hi, 16), lo); } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. words[nwords++] = 128; # 0x80 } else { # append a '1' bit in the byte just after the last input byte. words[nwords - 1] = bw_or(words[nwords - 1], bw_lshift(128, (nbytes % 4) * 8)); # 0x80 } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. while ((nwords % 16) != 14) nwords++; # Step 2. Append Length hi = bw_rshift(nbytes * 8, 32); lo = (nbytes * 8) - bw_lshift(hi, 32); words[nwords++] = lo; words[nwords++] = mod32bits(hi); # truncate to 32 bits # Step 3. Initialize MD Buffer state[0] = 1732584193; # 0x67452301 state[1] = 4023233417; # 0xefcdab89 state[2] = 2562383102; # 0x98badcfe state[3] = 271733878; # 0x10325476 # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. for (i = 0; i < nwords; i += 16) { # Copy block i into x. for (j = 0; j < 16; j++) x[j] = words[i + j]; a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 a = FF(a, b, c, d, x[ 0], S11, 3614090360); # 0xd76aa478 d = FF(d, a, b, c, x[ 1], S12, 3905402710); # 0xe8c7b756 c = FF(c, d, a, b, x[ 2], S13, 606105819); # 0x242070db b = FF(b, c, d, a, x[ 3], S14, 3250441966); # 0xc1bdceee a = FF(a, b, c, d, x[ 4], S11, 4118548399); # 0xf57c0faf d = FF(d, a, b, c, x[ 5], S12, 1200080426); # 0x4787c62a c = FF(c, d, a, b, x[ 6], S13, 2821735955); # 0xa8304613 b = FF(b, c, d, a, x[ 7], S14, 4249261313); # 0xfd469501 a = FF(a, b, c, d, x[ 8], S11, 1770035416); # 0x698098d8 d = FF(d, a, b, c, x[ 9], S12, 2336552879); # 0x8b44f7af c = FF(c, d, a, b, x[10], S13, 4294925233); # 0xffff5bb1 b = FF(b, c, d, a, x[11], S14, 2304563134); # 0x895cd7be a = FF(a, b, c, d, x[12], S11, 1804603682); # 0x6b901122 d = FF(d, a, b, c, x[13], S12, 4254626195); # 0xfd987193 c = FF(c, d, a, b, x[14], S13, 2792965006); # 0xa679438e b = FF(b, c, d, a, x[15], S14, 1236535329); # 0x49b40821 # Round 2 a = GG(a, b, c, d, x[ 1], S21, 4129170786); # 0xf61e2562 d = GG(d, a, b, c, x[ 6], S22, 3225465664); # 0xc040b340 c = GG(c, d, a, b, x[11], S23, 643717713); # 0x265e5a51 b = GG(b, c, d, a, x[ 0], S24, 3921069994); # 0xe9b6c7aa a = GG(a, b, c, d, x[ 5], S21, 3593408605); # 0xd62f105d d = GG(d, a, b, c, x[10], S22, 38016083); # 0x2441453 c = GG(c, d, a, b, x[15], S23, 3634488961); # 0xd8a1e681 b = GG(b, c, d, a, x[ 4], S24, 3889429448); # 0xe7d3fbc8 a = GG(a, b, c, d, x[ 9], S21, 568446438); # 0x21e1cde6 d = GG(d, a, b, c, x[14], S22, 3275163606); # 0xc33707d6 c = GG(c, d, a, b, x[ 3], S23, 4107603335); # 0xf4d50d87 b = GG(b, c, d, a, x[ 8], S24, 1163531501); # 0x455a14ed a = GG(a, b, c, d, x[13], S21, 2850285829); # 0xa9e3e905 d = GG(d, a, b, c, x[ 2], S22, 4243563512); # 0xfcefa3f8 c = GG(c, d, a, b, x[ 7], S23, 1735328473); # 0x676f02d9 b = GG(b, c, d, a, x[12], S24, 2368359562); # 0x8d2a4c8a # Round 3 a = HH(a, b, c, d, x[ 5], S31, 4294588738); # 0xfffa3942 d = HH(d, a, b, c, x[ 8], S32, 2272392833); # 0x8771f681 c = HH(c, d, a, b, x[11], S33, 1839030562); # 0x6d9d6122 b = HH(b, c, d, a, x[14], S34, 4259657740); # 0xfde5380c a = HH(a, b, c, d, x[ 1], S31, 2763975236); # 0xa4beea44 d = HH(d, a, b, c, x[ 4], S32, 1272893353); # 0x4bdecfa9 c = HH(c, d, a, b, x[ 7], S33, 4139469664); # 0xf6bb4b60 b = HH(b, c, d, a, x[10], S34, 3200236656); # 0xbebfbc70 a = HH(a, b, c, d, x[13], S31, 681279174); # 0x289b7ec6 d = HH(d, a, b, c, x[ 0], S32, 3936430074); # 0xeaa127fa c = HH(c, d, a, b, x[ 3], S33, 3572445317); # 0xd4ef3085 b = HH(b, c, d, a, x[ 6], S34, 76029189); # 0x4881d05 a = HH(a, b, c, d, x[ 9], S31, 3654602809); # 0xd9d4d039 d = HH(d, a, b, c, x[12], S32, 3873151461); # 0xe6db99e5 c = HH(c, d, a, b, x[15], S33, 530742520); # 0x1fa27cf8 b = HH(b, c, d, a, x[ 2], S34, 3299628645); # 0xc4ac5665 # Round 4 a = II(a, b, c, d, x[ 0], S41, 4096336452); # 0xf4292244 d = II(d, a, b, c, x[ 7], S42, 1126891415); # 0x432aff97 c = II(c, d, a, b, x[14], S43, 2878612391); # 0xab9423a7 b = II(b, c, d, a, x[ 5], S44, 4237533241); # 0xfc93a039 a = II(a, b, c, d, x[12], S41, 1700485571); # 0x655b59c3 d = II(d, a, b, c, x[ 3], S42, 2399980690); # 0x8f0ccc92 c = II(c, d, a, b, x[10], S43, 4293915773); # 0xffeff47d b = II(b, c, d, a, x[ 1], S44, 2240044497); # 0x85845dd1 a = II(a, b, c, d, x[ 8], S41, 1873313359); # 0x6fa87e4f d = II(d, a, b, c, x[15], S42, 4264355552); # 0xfe2ce6e0 c = II(c, d, a, b, x[ 6], S43, 2734768916); # 0xa3014314 b = II(b, c, d, a, x[13], S44, 1309151649); # 0x4e0811a1 a = II(a, b, c, d, x[ 4], S41, 4149444226); # 0xf7537e82 d = II(d, a, b, c, x[11], S42, 3174756917); # 0xbd3af235 c = II(c, d, a, b, x[ 2], S43, 718787259); # 0x2ad7d2bb b = II(b, c, d, a, x[ 9], S44, 3951481745); # 0xeb86d391 state[0] = mod32bits(state[0] + a); state[1] = mod32bits(state[1] + b); state[2] = mod32bits(state[2] + c); state[3] = mod32bits(state[3] + d); } for (i = j = 0; j < 16; j += 4) { digest[j + 0] = bw_and(state[i], 255); # 0xff digest[j + 1] = bw_and(bw_rshift(state[i], 8), 255); # 0xff digest[j + 2] = bw_and(bw_rshift(state[i], 16), 255); # 0xff digest[j + 3] = bw_and(bw_rshift(state[i++], 24), 255); # 0xff } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); return ret; } function F(x, y, z) { return bw_or(bw_and(x, y), bw_and(bw_not(x), z)); } function G(x, y, z) { return bw_or(bw_and(x, z), bw_and(y, bw_not(z))); } function H(x, y, z) { return bw_xor(x, bw_xor(y, z)); } function I(x, y, z) { return bw_xor(y, bw_or(x, bw_not(z))); } function FF(a, b, c, d, x, s, ac) { a = mod32bits(a + F(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function GG(a, b, c, d, x, s, ac) { a = mod32bits(a + G(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function HH(a, b, c, d, x, s, ac) { a = mod32bits(a + H(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function II(a, b, c, d, x, s, ac) { a = mod32bits(a + I(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function ROTATE_LEFT(x, n) { return bw_or(mod32bits(bw_lshift(x, n)), bw_rshift(x, 32 - n)); } function mod32bits(x) { return bw_and(x, 4294967295); # 0xffffffff } function bw_not(x) { return mod32bits(compl(x)); } function bw_lshift(x, n) { return x * (2 ^ n); } function bw_rshift(x, n) { return int(x / (2 ^ n)); } function bw_and(x, y) { return and(x, y); } function bw_or(x, y) { return or(x, y); } function bw_xor(x, y) { return xor(x, y); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } function _md5_init() { # MD5 shift constants setup. S11 = 7; S12 = 12; S13 = 17; S14 = 22; S21 = 5; S22 = 9; S23 = 14; S24 = 20; S31 = 4; S32 = 11; S33 = 16; S34 = 23; S41 = 6; S42 = 10; S43 = 15; S44 = 21; } |
diff -u step3.awk step4.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | --- step3.awk 2017-02-20 21:30:13.502377000 +0100 +++ step4.awk 2017-02-20 21:30:23.464046000 +0100 @@ -218,11 +218,11 @@ } function bw_lshift(x, n) { - return lshift(x, n); + return x * (2 ^ n); } function bw_rshift(x, n) { - return rshift(x, n); + return int(x / (2 ^ n)); } function bw_and(x, y) { |
Surprisingly (at least to me), AWK has an exponentiation operator
^ making computing power of two trivial.
Note that since GNU Awk lshift
may yield a number that is greater than 2^32 we already ensure to
mod32bits its result where needed (in ROTATE_LEFT).
Thus, our bw_lshift doesn't have to hold this invariant. Because
AWK division is a "real division" (i.e. not an integer division) we need to
drop the fractional part from bw_rshift's result, hence the
int() truncation.
% time gawk -f step4.awk sqlite-src-3160200/src/* | tee /tmp/step4.out
...
gawk -f step4.awk sqlite-src-3160200/src/* 25.50s user 0.20s system 100% cpu 25.687 total
tee /tmp/step4.out 0.00s user 0.00s system 0% cpu 25.687 total
The running time increased by "only" about 3%, which is less that I
personally expected. My best guess is that lshift and
rshift are actually slower than what "we think" (we usually see
them as fast), because of the number representation dance that
GNU Awk has to do (from double to
uintmax_t and then back to double).
and, or, xor & not
Intuitively I thought about iterating through each bit using %
and shifting. Although this should "do the trick" it is awfully slow:
example of bw_and() bit by bit
1 2 3 4 5 6 7 8 | function bw_and(x, y, i, r) { for (i = 0; i < 32; i++) { r += ((x % 2) && (y % 2)) * (2 ^ i); x = int(x / 2); y = int(y / 2); } return r; } |
Line 3 can easily be adapted to implement bw_or,
bw_xor and bw_not.
Seeking a better solution, I found this helpful StackOverflow answer. The AND solution described looks promising: by using a lookup table for each combination of 4 x 4 bits of input we only have to loop 8 times (instead of 32). Additionally, XOR and OR are elegantly implemented on top of AND.
Instead of using a pre-computed lookup table, I've opted for bootstrapping it
using the slow bit-by-bit method. This will be more consistent with
_ord_init, yield cleaner and smaller code, and just feels more
in tune with the "pure AWK" vision that is the raison d'être of this
implementation.
Here is our version, translated in AWK (using multiple array subscripts) and tweaked a bit (because the StackOverflow answer was for 16-bits numbers and we use 32-bits).
step5.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 | BEGIN { _ord_init(); _bitwise_init(); _md5_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, a, b, c, d, j, x, digest, ret) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = bw_or(bw_lshift(bytes[i + 3], 8), bytes[i + 2]); lo = bw_or(bw_lshift(bytes[i + 1], 8), bytes[i + 0]); words[nwords++] = bw_or(bw_lshift(hi, 16), lo); } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. words[nwords++] = 128; # 0x80 } else { # append a '1' bit in the byte just after the last input byte. words[nwords - 1] = bw_or(words[nwords - 1], bw_lshift(128, (nbytes % 4) * 8)); # 0x80 } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. while ((nwords % 16) != 14) nwords++; # Step 2. Append Length hi = bw_rshift(nbytes * 8, 32); lo = (nbytes * 8) - bw_lshift(hi, 32); words[nwords++] = lo; words[nwords++] = mod32bits(hi); # truncate to 32 bits # Step 3. Initialize MD Buffer state[0] = 1732584193; # 0x67452301 state[1] = 4023233417; # 0xefcdab89 state[2] = 2562383102; # 0x98badcfe state[3] = 271733878; # 0x10325476 # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. for (i = 0; i < nwords; i += 16) { # Copy block i into x. for (j = 0; j < 16; j++) x[j] = words[i + j]; a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 a = FF(a, b, c, d, x[ 0], S11, 3614090360); # 0xd76aa478 d = FF(d, a, b, c, x[ 1], S12, 3905402710); # 0xe8c7b756 c = FF(c, d, a, b, x[ 2], S13, 606105819); # 0x242070db b = FF(b, c, d, a, x[ 3], S14, 3250441966); # 0xc1bdceee a = FF(a, b, c, d, x[ 4], S11, 4118548399); # 0xf57c0faf d = FF(d, a, b, c, x[ 5], S12, 1200080426); # 0x4787c62a c = FF(c, d, a, b, x[ 6], S13, 2821735955); # 0xa8304613 b = FF(b, c, d, a, x[ 7], S14, 4249261313); # 0xfd469501 a = FF(a, b, c, d, x[ 8], S11, 1770035416); # 0x698098d8 d = FF(d, a, b, c, x[ 9], S12, 2336552879); # 0x8b44f7af c = FF(c, d, a, b, x[10], S13, 4294925233); # 0xffff5bb1 b = FF(b, c, d, a, x[11], S14, 2304563134); # 0x895cd7be a = FF(a, b, c, d, x[12], S11, 1804603682); # 0x6b901122 d = FF(d, a, b, c, x[13], S12, 4254626195); # 0xfd987193 c = FF(c, d, a, b, x[14], S13, 2792965006); # 0xa679438e b = FF(b, c, d, a, x[15], S14, 1236535329); # 0x49b40821 # Round 2 a = GG(a, b, c, d, x[ 1], S21, 4129170786); # 0xf61e2562 d = GG(d, a, b, c, x[ 6], S22, 3225465664); # 0xc040b340 c = GG(c, d, a, b, x[11], S23, 643717713); # 0x265e5a51 b = GG(b, c, d, a, x[ 0], S24, 3921069994); # 0xe9b6c7aa a = GG(a, b, c, d, x[ 5], S21, 3593408605); # 0xd62f105d d = GG(d, a, b, c, x[10], S22, 38016083); # 0x2441453 c = GG(c, d, a, b, x[15], S23, 3634488961); # 0xd8a1e681 b = GG(b, c, d, a, x[ 4], S24, 3889429448); # 0xe7d3fbc8 a = GG(a, b, c, d, x[ 9], S21, 568446438); # 0x21e1cde6 d = GG(d, a, b, c, x[14], S22, 3275163606); # 0xc33707d6 c = GG(c, d, a, b, x[ 3], S23, 4107603335); # 0xf4d50d87 b = GG(b, c, d, a, x[ 8], S24, 1163531501); # 0x455a14ed a = GG(a, b, c, d, x[13], S21, 2850285829); # 0xa9e3e905 d = GG(d, a, b, c, x[ 2], S22, 4243563512); # 0xfcefa3f8 c = GG(c, d, a, b, x[ 7], S23, 1735328473); # 0x676f02d9 b = GG(b, c, d, a, x[12], S24, 2368359562); # 0x8d2a4c8a # Round 3 a = HH(a, b, c, d, x[ 5], S31, 4294588738); # 0xfffa3942 d = HH(d, a, b, c, x[ 8], S32, 2272392833); # 0x8771f681 c = HH(c, d, a, b, x[11], S33, 1839030562); # 0x6d9d6122 b = HH(b, c, d, a, x[14], S34, 4259657740); # 0xfde5380c a = HH(a, b, c, d, x[ 1], S31, 2763975236); # 0xa4beea44 d = HH(d, a, b, c, x[ 4], S32, 1272893353); # 0x4bdecfa9 c = HH(c, d, a, b, x[ 7], S33, 4139469664); # 0xf6bb4b60 b = HH(b, c, d, a, x[10], S34, 3200236656); # 0xbebfbc70 a = HH(a, b, c, d, x[13], S31, 681279174); # 0x289b7ec6 d = HH(d, a, b, c, x[ 0], S32, 3936430074); # 0xeaa127fa c = HH(c, d, a, b, x[ 3], S33, 3572445317); # 0xd4ef3085 b = HH(b, c, d, a, x[ 6], S34, 76029189); # 0x4881d05 a = HH(a, b, c, d, x[ 9], S31, 3654602809); # 0xd9d4d039 d = HH(d, a, b, c, x[12], S32, 3873151461); # 0xe6db99e5 c = HH(c, d, a, b, x[15], S33, 530742520); # 0x1fa27cf8 b = HH(b, c, d, a, x[ 2], S34, 3299628645); # 0xc4ac5665 # Round 4 a = II(a, b, c, d, x[ 0], S41, 4096336452); # 0xf4292244 d = II(d, a, b, c, x[ 7], S42, 1126891415); # 0x432aff97 c = II(c, d, a, b, x[14], S43, 2878612391); # 0xab9423a7 b = II(b, c, d, a, x[ 5], S44, 4237533241); # 0xfc93a039 a = II(a, b, c, d, x[12], S41, 1700485571); # 0x655b59c3 d = II(d, a, b, c, x[ 3], S42, 2399980690); # 0x8f0ccc92 c = II(c, d, a, b, x[10], S43, 4293915773); # 0xffeff47d b = II(b, c, d, a, x[ 1], S44, 2240044497); # 0x85845dd1 a = II(a, b, c, d, x[ 8], S41, 1873313359); # 0x6fa87e4f d = II(d, a, b, c, x[15], S42, 4264355552); # 0xfe2ce6e0 c = II(c, d, a, b, x[ 6], S43, 2734768916); # 0xa3014314 b = II(b, c, d, a, x[13], S44, 1309151649); # 0x4e0811a1 a = II(a, b, c, d, x[ 4], S41, 4149444226); # 0xf7537e82 d = II(d, a, b, c, x[11], S42, 3174756917); # 0xbd3af235 c = II(c, d, a, b, x[ 2], S43, 718787259); # 0x2ad7d2bb b = II(b, c, d, a, x[ 9], S44, 3951481745); # 0xeb86d391 state[0] = mod32bits(state[0] + a); state[1] = mod32bits(state[1] + b); state[2] = mod32bits(state[2] + c); state[3] = mod32bits(state[3] + d); } for (i = j = 0; j < 16; j += 4) { digest[j + 0] = bw_and(state[i], 255); # 0xff digest[j + 1] = bw_and(bw_rshift(state[i], 8), 255); # 0xff digest[j + 2] = bw_and(bw_rshift(state[i], 16), 255); # 0xff digest[j + 3] = bw_and(bw_rshift(state[i++], 24), 255); # 0xff } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); return ret; } function F(x, y, z) { return bw_or(bw_and(x, y), bw_and(bw_not(x), z)); } function G(x, y, z) { return bw_or(bw_and(x, z), bw_and(y, bw_not(z))); } function H(x, y, z) { return bw_xor(x, bw_xor(y, z)); } function I(x, y, z) { return bw_xor(y, bw_or(x, bw_not(z))); } function FF(a, b, c, d, x, s, ac) { a = mod32bits(a + F(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function GG(a, b, c, d, x, s, ac) { a = mod32bits(a + G(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function HH(a, b, c, d, x, s, ac) { a = mod32bits(a + H(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function II(a, b, c, d, x, s, ac) { a = mod32bits(a + I(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function ROTATE_LEFT(x, n) { return bw_or(mod32bits(bw_lshift(x, n)), bw_rshift(x, 32 - n)); } function mod32bits(x) { return bw_and(x, 4294967295); # 0xffffffff } function bw_not(x) { return bw_xor(x, 4294967295); # 0xffffffff } function bw_lshift(x, n) { return x * (2 ^ n); } function bw_rshift(x, n) { return int(x / (2 ^ n)); } function bw_and(x, y, i, r) { for (i = 0; i < 32; i += 4) { r = r / (2 ^ 4) + andlookup[x % 16, y % 16] * (2 ^ 28); x = int(x / (2 ^ 4)); y = int(y / (2 ^ 4)); } return r; } function bw_or(x, y) { return bw_xor(bw_xor(x, y), bw_and(x, y)); } function bw_xor(x, y) { return (x + y - 2 * bw_and(x, y)); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } function _bitwise_init( a, b, x, y, i) { # generate the lookup table for bw_and(). for (a = 0; a < 16; a++) { for (b = 0; b < 16; b++) { x = a; y = b; for (i = 0; i < 4; i++) { andlookup[a, b] += ((x % 2) && (y % 2)) * (2 ^ i); x = int(x / 2); y = int(y / 2); } } } } function _md5_init() { # MD5 shift constants setup. S11 = 7; S12 = 12; S13 = 17; S14 = 22; S21 = 5; S22 = 9; S23 = 14; S24 = 20; S31 = 4; S32 = 11; S33 = 16; S34 = 23; S41 = 6; S42 = 10; S43 = 15; S44 = 21; } |
diff -u step4.awk step5.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 | --- step4.awk 2017-02-20 21:30:23.464046000 +0100 +++ step5.awk 2017-02-21 14:58:31.499103000 +0100 @@ -1,5 +1,6 @@ BEGIN { _ord_init(); + _bitwise_init(); _md5_init(); } @@ -214,7 +215,7 @@ } function bw_not(x) { - return mod32bits(compl(x)); + return bw_xor(x, 4294967295); # 0xffffffff } function bw_lshift(x, n) { @@ -225,16 +226,21 @@ return int(x / (2 ^ n)); } -function bw_and(x, y) { - return and(x, y); +function bw_and(x, y, i, r) { + for (i = 0; i < 32; i += 4) { + r = r / (2 ^ 4) + andlookup[x % 16, y % 16] * (2 ^ 28); + x = int(x / (2 ^ 4)); + y = int(y / (2 ^ 4)); + } + return r; } function bw_or(x, y) { - return or(x, y); + return bw_xor(bw_xor(x, y), bw_and(x, y)); } function bw_xor(x, y) { - return xor(x, y); + return (x + y - 2 * bw_and(x, y)); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html @@ -250,6 +256,21 @@ return _ord_[substr(s, 1, 1)]; } +function _bitwise_init( a, b, x, y, i) { + # generate the lookup table for bw_and(). + for (a = 0; a < 16; a++) { + for (b = 0; b < 16; b++) { + x = a; + y = b; + for (i = 0; i < 4; i++) { + andlookup[a, b] += ((x % 2) && (y % 2)) * (2 ^ i); + x = int(x / 2); + y = int(y / 2); + } + } + } +} + function _md5_init() { # MD5 shift constants setup. S11 = 7; S12 = 12; S13 = 17; S14 = 22; |
Let's test our changes:
% time gawk -f step5.awk sqlite-src-3160200/src/* | tee /tmp/step5.out
...
gawk -f step5.awk sqlite-src-3160200/src/* 541.14s user 0.19s system 100% cpu 9:01.32 total
tee /tmp/step5.out 0.00s user 0.00s system 0% cpu 9:01.32 totalNow the good news is that our script doesn't use GNU Awk bitwise function anymore, and consequently we can also test with one-true-awk too:
% time awk -f step5.awk sqlite-src-3160200/src/* | tee /tmp/step5.out
...
awk -f step5.awk sqlite-src-3160200/src/* 1164.34s user 0.96s system 100% cpu 19:25.19 total
tee /tmp/step5.out 0.00s user 0.00s system 0% cpu 19:25.19 totalYay! We've succeeded in our attempt to implement MD5 in AWK! That's a big step as we can test with several AWK implementations from now on. At this point though, the performances are horrible even for my coding challenge context: the script is roughly 20 times slower than the previous version. Also worth noting, GNU Awk is about two times faster than one-true-awk for this test.
Improvements
While we didn't worry too much about performances in our porting steps, we've kept an eye on the impact of each change. Thus, we should have a good idea of what should be improved, but let's run our script through GNU Awk's profiler anyway (yes, it has one):
profiling
% gawk --profile=step5.prof -f step5.awk sqlite-src-3160200/src/* | tee /tmp/step5.out
% awk '$2 == "function" {print}' step5.prof | sort -n
1 function _bitwise_init(a, b, x, y, i)
1 function _md5_init()
1 function _ord_init(i)
149 function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, a, b, c, d, j, x, digest, ret)
1586192 function FF(a, b, c, d, x, s, ac)
1586192 function F(x, y, z)
1586192 function GG(a, b, c, d, x, s, ac)
1586192 function G(x, y, z)
1586192 function HH(a, b, c, d, x, s, ac)
1586192 function H(x, y, z)
1586192 function II(a, b, c, d, x, s, ac)
1586192 function I(x, y, z)
4758576 function bw_not(x)
6338697 function ord(s)
6344768 function ROTATE_LEFT(x, n)
6346705 function bw_rshift(x, n)
11099214 function bw_lshift(x, n)
15857641 function bw_or(x, y)
19431001 function mod32bits(x)
41232434 function bw_xor(x, y)
82868228 function bw_and(x, y, i, r)For something more visual, here is a (handmade by yours truly) callgraph:
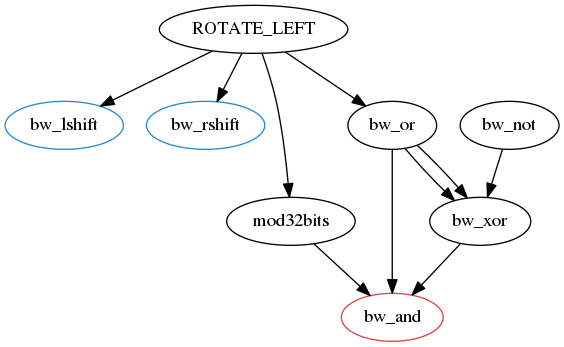
step5.dot
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | digraph G { ROTATE_LEFT -> bw_lshift; ROTATE_LEFT -> bw_rshift; ROTATE_LEFT -> mod32bits; ROTATE_LEFT -> bw_or; mod32bits -> bw_and; bw_not -> bw_xor; bw_or -> bw_xor; bw_or -> bw_xor; bw_or -> bw_and; bw_xor -> bw_and; bw_and [color="#dd4444"]; bw_lshift [color="#268bd2"]; bw_rshift [color="#268bd2"]; } |
We see that there is a ton of pressure on bw_and. Sadly, the
profiler is only able to report how many time each function was called. The
running time of each function would have been very useful, but we'll have to
"play it by ear". From the timings we gathered so far we think that:
- From step3.awk we learned that calling functions is costly.
-
step4.awk showed that both
bw_lshiftandbw_rshiftperformances are close to before porting, so they're not on our radar to optimize (hence the blue color in the callgraph). -
Since step5.awk
bw_andhas become really slow (hence the red color in the callgraph), but we think the memory vs runtime tradeoff is acceptable.
bw_or
Obviously our bw_or function can be improved: it calls
bw_xor twice and bw_and once, for a total of "3
times bw_and cost". The most straightforward refactoring is to
mimic bw_and implementation and should make bw_or
three time faster:
step6.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 | BEGIN { _ord_init(); _bitwise_init(); _md5_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, a, b, c, d, j, x, digest, ret) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = bw_or(bw_lshift(bytes[i + 3], 8), bytes[i + 2]); lo = bw_or(bw_lshift(bytes[i + 1], 8), bytes[i + 0]); words[nwords++] = bw_or(bw_lshift(hi, 16), lo); } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. words[nwords++] = 128; # 0x80 } else { # append a '1' bit in the byte just after the last input byte. words[nwords - 1] = bw_or(words[nwords - 1], bw_lshift(128, (nbytes % 4) * 8)); # 0x80 } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. while ((nwords % 16) != 14) nwords++; # Step 2. Append Length hi = bw_rshift(nbytes * 8, 32); lo = (nbytes * 8) - bw_lshift(hi, 32); words[nwords++] = lo; words[nwords++] = mod32bits(hi); # truncate to 32 bits # Step 3. Initialize MD Buffer state[0] = 1732584193; # 0x67452301 state[1] = 4023233417; # 0xefcdab89 state[2] = 2562383102; # 0x98badcfe state[3] = 271733878; # 0x10325476 # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. for (i = 0; i < nwords; i += 16) { # Copy block i into x. for (j = 0; j < 16; j++) x[j] = words[i + j]; a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 a = FF(a, b, c, d, x[ 0], S11, 3614090360); # 0xd76aa478 d = FF(d, a, b, c, x[ 1], S12, 3905402710); # 0xe8c7b756 c = FF(c, d, a, b, x[ 2], S13, 606105819); # 0x242070db b = FF(b, c, d, a, x[ 3], S14, 3250441966); # 0xc1bdceee a = FF(a, b, c, d, x[ 4], S11, 4118548399); # 0xf57c0faf d = FF(d, a, b, c, x[ 5], S12, 1200080426); # 0x4787c62a c = FF(c, d, a, b, x[ 6], S13, 2821735955); # 0xa8304613 b = FF(b, c, d, a, x[ 7], S14, 4249261313); # 0xfd469501 a = FF(a, b, c, d, x[ 8], S11, 1770035416); # 0x698098d8 d = FF(d, a, b, c, x[ 9], S12, 2336552879); # 0x8b44f7af c = FF(c, d, a, b, x[10], S13, 4294925233); # 0xffff5bb1 b = FF(b, c, d, a, x[11], S14, 2304563134); # 0x895cd7be a = FF(a, b, c, d, x[12], S11, 1804603682); # 0x6b901122 d = FF(d, a, b, c, x[13], S12, 4254626195); # 0xfd987193 c = FF(c, d, a, b, x[14], S13, 2792965006); # 0xa679438e b = FF(b, c, d, a, x[15], S14, 1236535329); # 0x49b40821 # Round 2 a = GG(a, b, c, d, x[ 1], S21, 4129170786); # 0xf61e2562 d = GG(d, a, b, c, x[ 6], S22, 3225465664); # 0xc040b340 c = GG(c, d, a, b, x[11], S23, 643717713); # 0x265e5a51 b = GG(b, c, d, a, x[ 0], S24, 3921069994); # 0xe9b6c7aa a = GG(a, b, c, d, x[ 5], S21, 3593408605); # 0xd62f105d d = GG(d, a, b, c, x[10], S22, 38016083); # 0x2441453 c = GG(c, d, a, b, x[15], S23, 3634488961); # 0xd8a1e681 b = GG(b, c, d, a, x[ 4], S24, 3889429448); # 0xe7d3fbc8 a = GG(a, b, c, d, x[ 9], S21, 568446438); # 0x21e1cde6 d = GG(d, a, b, c, x[14], S22, 3275163606); # 0xc33707d6 c = GG(c, d, a, b, x[ 3], S23, 4107603335); # 0xf4d50d87 b = GG(b, c, d, a, x[ 8], S24, 1163531501); # 0x455a14ed a = GG(a, b, c, d, x[13], S21, 2850285829); # 0xa9e3e905 d = GG(d, a, b, c, x[ 2], S22, 4243563512); # 0xfcefa3f8 c = GG(c, d, a, b, x[ 7], S23, 1735328473); # 0x676f02d9 b = GG(b, c, d, a, x[12], S24, 2368359562); # 0x8d2a4c8a # Round 3 a = HH(a, b, c, d, x[ 5], S31, 4294588738); # 0xfffa3942 d = HH(d, a, b, c, x[ 8], S32, 2272392833); # 0x8771f681 c = HH(c, d, a, b, x[11], S33, 1839030562); # 0x6d9d6122 b = HH(b, c, d, a, x[14], S34, 4259657740); # 0xfde5380c a = HH(a, b, c, d, x[ 1], S31, 2763975236); # 0xa4beea44 d = HH(d, a, b, c, x[ 4], S32, 1272893353); # 0x4bdecfa9 c = HH(c, d, a, b, x[ 7], S33, 4139469664); # 0xf6bb4b60 b = HH(b, c, d, a, x[10], S34, 3200236656); # 0xbebfbc70 a = HH(a, b, c, d, x[13], S31, 681279174); # 0x289b7ec6 d = HH(d, a, b, c, x[ 0], S32, 3936430074); # 0xeaa127fa c = HH(c, d, a, b, x[ 3], S33, 3572445317); # 0xd4ef3085 b = HH(b, c, d, a, x[ 6], S34, 76029189); # 0x4881d05 a = HH(a, b, c, d, x[ 9], S31, 3654602809); # 0xd9d4d039 d = HH(d, a, b, c, x[12], S32, 3873151461); # 0xe6db99e5 c = HH(c, d, a, b, x[15], S33, 530742520); # 0x1fa27cf8 b = HH(b, c, d, a, x[ 2], S34, 3299628645); # 0xc4ac5665 # Round 4 a = II(a, b, c, d, x[ 0], S41, 4096336452); # 0xf4292244 d = II(d, a, b, c, x[ 7], S42, 1126891415); # 0x432aff97 c = II(c, d, a, b, x[14], S43, 2878612391); # 0xab9423a7 b = II(b, c, d, a, x[ 5], S44, 4237533241); # 0xfc93a039 a = II(a, b, c, d, x[12], S41, 1700485571); # 0x655b59c3 d = II(d, a, b, c, x[ 3], S42, 2399980690); # 0x8f0ccc92 c = II(c, d, a, b, x[10], S43, 4293915773); # 0xffeff47d b = II(b, c, d, a, x[ 1], S44, 2240044497); # 0x85845dd1 a = II(a, b, c, d, x[ 8], S41, 1873313359); # 0x6fa87e4f d = II(d, a, b, c, x[15], S42, 4264355552); # 0xfe2ce6e0 c = II(c, d, a, b, x[ 6], S43, 2734768916); # 0xa3014314 b = II(b, c, d, a, x[13], S44, 1309151649); # 0x4e0811a1 a = II(a, b, c, d, x[ 4], S41, 4149444226); # 0xf7537e82 d = II(d, a, b, c, x[11], S42, 3174756917); # 0xbd3af235 c = II(c, d, a, b, x[ 2], S43, 718787259); # 0x2ad7d2bb b = II(b, c, d, a, x[ 9], S44, 3951481745); # 0xeb86d391 state[0] = mod32bits(state[0] + a); state[1] = mod32bits(state[1] + b); state[2] = mod32bits(state[2] + c); state[3] = mod32bits(state[3] + d); } for (i = j = 0; j < 16; j += 4) { digest[j + 0] = bw_and(state[i], 255); # 0xff digest[j + 1] = bw_and(bw_rshift(state[i], 8), 255); # 0xff digest[j + 2] = bw_and(bw_rshift(state[i], 16), 255); # 0xff digest[j + 3] = bw_and(bw_rshift(state[i++], 24), 255); # 0xff } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); return ret; } function F(x, y, z) { return bw_or(bw_and(x, y), bw_and(bw_not(x), z)); } function G(x, y, z) { return bw_or(bw_and(x, z), bw_and(y, bw_not(z))); } function H(x, y, z) { return bw_xor(x, bw_xor(y, z)); } function I(x, y, z) { return bw_xor(y, bw_or(x, bw_not(z))); } function FF(a, b, c, d, x, s, ac) { a = mod32bits(a + F(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function GG(a, b, c, d, x, s, ac) { a = mod32bits(a + G(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function HH(a, b, c, d, x, s, ac) { a = mod32bits(a + H(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function II(a, b, c, d, x, s, ac) { a = mod32bits(a + I(b, c, d) + x + ac); a = ROTATE_LEFT(a, s); a = mod32bits(a + b); return a; } function ROTATE_LEFT(x, n) { return bw_or(mod32bits(bw_lshift(x, n)), bw_rshift(x, 32 - n)); } function mod32bits(x) { return bw_and(x, 4294967295); # 0xffffffff } function bw_not(x) { return bw_xor(x, 4294967295); # 0xffffffff } function bw_lshift(x, n) { return x * (2 ^ n); } function bw_rshift(x, n) { return int(x / (2 ^ n)); } function bw_and(x, y, i, r) { for (i = 0; i < 32; i += 4) { r = r / (2 ^ 4) + bw_lookup["and", x % 16, y % 16] * (2 ^ 28); x = int(x / (2 ^ 4)); y = int(y / (2 ^ 4)); } return r; } function bw_or(x, y, i, r) { for (i = 0; i < 32; i += 4) { r = r / (2 ^ 4) + bw_lookup["or", x % 16, y % 16] * (2 ^ 28); x = int(x / (2 ^ 4)); y = int(y / (2 ^ 4)); } return r; } function bw_xor(x, y) { return (x + y - 2 * bw_and(x, y)); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } function _bitwise_init( a, b, x, y, i) { # generate the bw_lookup table used by bw_and() and bw_or(). for (a = 0; a < 16; a++) { for (b = 0; b < 16; b++) { x = a; y = b; for (i = 0; i < 4; i++) { bw_lookup["and", a, b] += ((x % 2) && (y % 2)) * (2 ^ i); bw_lookup["or", a, b] += ((x % 2) || (y % 2)) * (2 ^ i); x = int(x / 2); y = int(y / 2); } } } } function _md5_init() { # MD5 shift constants setup. S11 = 7; S12 = 12; S13 = 17; S14 = 22; S21 = 5; S22 = 9; S23 = 14; S24 = 20; S31 = 4; S32 = 11; S33 = 16; S34 = 23; S41 = 6; S42 = 10; S43 = 15; S44 = 21; } |
diff -u step5.awk step6.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | --- step5.awk 2017-02-21 14:58:31.499103000 +0100 +++ step6.awk 2017-03-04 12:57:02.936165000 +0100 @@ -228,15 +228,20 @@ function bw_and(x, y, i, r) { for (i = 0; i < 32; i += 4) { - r = r / (2 ^ 4) + andlookup[x % 16, y % 16] * (2 ^ 28); + r = r / (2 ^ 4) + bw_lookup["and", x % 16, y % 16] * (2 ^ 28); x = int(x / (2 ^ 4)); y = int(y / (2 ^ 4)); } return r; } -function bw_or(x, y) { - return bw_xor(bw_xor(x, y), bw_and(x, y)); +function bw_or(x, y, i, r) { + for (i = 0; i < 32; i += 4) { + r = r / (2 ^ 4) + bw_lookup["or", x % 16, y % 16] * (2 ^ 28); + x = int(x / (2 ^ 4)); + y = int(y / (2 ^ 4)); + } + return r; } function bw_xor(x, y) { @@ -257,13 +262,14 @@ } function _bitwise_init( a, b, x, y, i) { - # generate the lookup table for bw_and(). + # generate the bw_lookup table used by bw_and() and bw_or(). for (a = 0; a < 16; a++) { for (b = 0; b < 16; b++) { x = a; y = b; for (i = 0; i < 4; i++) { - andlookup[a, b] += ((x % 2) && (y % 2)) * (2 ^ i); + bw_lookup["and", a, b] += ((x % 2) && (y % 2)) * (2 ^ i); + bw_lookup["or", a, b] += ((x % 2) || (y % 2)) * (2 ^ i); x = int(x / 2); y = int(y / 2); } |
Although we could easily do the same for bw_not and
bw_xor, their "perceived bw_and cost" is 1, and so
there is not much to be gain. Let's see the impact of our change:
% time gawk -f step6.awk sqlite-src-3160200/src/* | tee /tmp/step6.out
...
gawk -f step6.awk sqlite-src-3160200/src/* 350.09s user 0.14s system 100% cpu 5:50.17 total
tee /tmp/step6.out 0.00s user 0.00s system 0% cpu 5:50.17 totalThat's a 35% improvement, well worth it. Let's focus now on the next "obvious" target.
mod32bits
Originally, we wrote mod32bits using and because it
was "fast". Now the modulo % operator is very likely to be
faster than bw_and and we can easily just get rid of the
mod32bits function:
step7.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 | BEGIN { _ord_init(); _bitwise_init(); _md5_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, a, b, c, d, j, x, digest, ret) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = bw_or(bw_lshift(bytes[i + 3], 8), bytes[i + 2]); lo = bw_or(bw_lshift(bytes[i + 1], 8), bytes[i + 0]); words[nwords++] = bw_or(bw_lshift(hi, 16), lo); } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. words[nwords++] = 128; # 0x80 } else { # append a '1' bit in the byte just after the last input byte. words[nwords - 1] = bw_or(words[nwords - 1], bw_lshift(128, (nbytes % 4) * 8)); # 0x80 } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. while ((nwords % 16) != 14) nwords++; # Step 2. Append Length hi = bw_rshift(nbytes * 8, 32); lo = (nbytes * 8) - bw_lshift(hi, 32); words[nwords++] = lo; words[nwords++] = hi % (2 ^ 32); # truncate to 32 bits # Step 3. Initialize MD Buffer state[0] = 1732584193; # 0x67452301 state[1] = 4023233417; # 0xefcdab89 state[2] = 2562383102; # 0x98badcfe state[3] = 271733878; # 0x10325476 # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. for (i = 0; i < nwords; i += 16) { # Copy block i into x. for (j = 0; j < 16; j++) x[j] = words[i + j]; a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 a = FF(a, b, c, d, x[ 0], S11, 3614090360); # 0xd76aa478 d = FF(d, a, b, c, x[ 1], S12, 3905402710); # 0xe8c7b756 c = FF(c, d, a, b, x[ 2], S13, 606105819); # 0x242070db b = FF(b, c, d, a, x[ 3], S14, 3250441966); # 0xc1bdceee a = FF(a, b, c, d, x[ 4], S11, 4118548399); # 0xf57c0faf d = FF(d, a, b, c, x[ 5], S12, 1200080426); # 0x4787c62a c = FF(c, d, a, b, x[ 6], S13, 2821735955); # 0xa8304613 b = FF(b, c, d, a, x[ 7], S14, 4249261313); # 0xfd469501 a = FF(a, b, c, d, x[ 8], S11, 1770035416); # 0x698098d8 d = FF(d, a, b, c, x[ 9], S12, 2336552879); # 0x8b44f7af c = FF(c, d, a, b, x[10], S13, 4294925233); # 0xffff5bb1 b = FF(b, c, d, a, x[11], S14, 2304563134); # 0x895cd7be a = FF(a, b, c, d, x[12], S11, 1804603682); # 0x6b901122 d = FF(d, a, b, c, x[13], S12, 4254626195); # 0xfd987193 c = FF(c, d, a, b, x[14], S13, 2792965006); # 0xa679438e b = FF(b, c, d, a, x[15], S14, 1236535329); # 0x49b40821 # Round 2 a = GG(a, b, c, d, x[ 1], S21, 4129170786); # 0xf61e2562 d = GG(d, a, b, c, x[ 6], S22, 3225465664); # 0xc040b340 c = GG(c, d, a, b, x[11], S23, 643717713); # 0x265e5a51 b = GG(b, c, d, a, x[ 0], S24, 3921069994); # 0xe9b6c7aa a = GG(a, b, c, d, x[ 5], S21, 3593408605); # 0xd62f105d d = GG(d, a, b, c, x[10], S22, 38016083); # 0x2441453 c = GG(c, d, a, b, x[15], S23, 3634488961); # 0xd8a1e681 b = GG(b, c, d, a, x[ 4], S24, 3889429448); # 0xe7d3fbc8 a = GG(a, b, c, d, x[ 9], S21, 568446438); # 0x21e1cde6 d = GG(d, a, b, c, x[14], S22, 3275163606); # 0xc33707d6 c = GG(c, d, a, b, x[ 3], S23, 4107603335); # 0xf4d50d87 b = GG(b, c, d, a, x[ 8], S24, 1163531501); # 0x455a14ed a = GG(a, b, c, d, x[13], S21, 2850285829); # 0xa9e3e905 d = GG(d, a, b, c, x[ 2], S22, 4243563512); # 0xfcefa3f8 c = GG(c, d, a, b, x[ 7], S23, 1735328473); # 0x676f02d9 b = GG(b, c, d, a, x[12], S24, 2368359562); # 0x8d2a4c8a # Round 3 a = HH(a, b, c, d, x[ 5], S31, 4294588738); # 0xfffa3942 d = HH(d, a, b, c, x[ 8], S32, 2272392833); # 0x8771f681 c = HH(c, d, a, b, x[11], S33, 1839030562); # 0x6d9d6122 b = HH(b, c, d, a, x[14], S34, 4259657740); # 0xfde5380c a = HH(a, b, c, d, x[ 1], S31, 2763975236); # 0xa4beea44 d = HH(d, a, b, c, x[ 4], S32, 1272893353); # 0x4bdecfa9 c = HH(c, d, a, b, x[ 7], S33, 4139469664); # 0xf6bb4b60 b = HH(b, c, d, a, x[10], S34, 3200236656); # 0xbebfbc70 a = HH(a, b, c, d, x[13], S31, 681279174); # 0x289b7ec6 d = HH(d, a, b, c, x[ 0], S32, 3936430074); # 0xeaa127fa c = HH(c, d, a, b, x[ 3], S33, 3572445317); # 0xd4ef3085 b = HH(b, c, d, a, x[ 6], S34, 76029189); # 0x4881d05 a = HH(a, b, c, d, x[ 9], S31, 3654602809); # 0xd9d4d039 d = HH(d, a, b, c, x[12], S32, 3873151461); # 0xe6db99e5 c = HH(c, d, a, b, x[15], S33, 530742520); # 0x1fa27cf8 b = HH(b, c, d, a, x[ 2], S34, 3299628645); # 0xc4ac5665 # Round 4 a = II(a, b, c, d, x[ 0], S41, 4096336452); # 0xf4292244 d = II(d, a, b, c, x[ 7], S42, 1126891415); # 0x432aff97 c = II(c, d, a, b, x[14], S43, 2878612391); # 0xab9423a7 b = II(b, c, d, a, x[ 5], S44, 4237533241); # 0xfc93a039 a = II(a, b, c, d, x[12], S41, 1700485571); # 0x655b59c3 d = II(d, a, b, c, x[ 3], S42, 2399980690); # 0x8f0ccc92 c = II(c, d, a, b, x[10], S43, 4293915773); # 0xffeff47d b = II(b, c, d, a, x[ 1], S44, 2240044497); # 0x85845dd1 a = II(a, b, c, d, x[ 8], S41, 1873313359); # 0x6fa87e4f d = II(d, a, b, c, x[15], S42, 4264355552); # 0xfe2ce6e0 c = II(c, d, a, b, x[ 6], S43, 2734768916); # 0xa3014314 b = II(b, c, d, a, x[13], S44, 1309151649); # 0x4e0811a1 a = II(a, b, c, d, x[ 4], S41, 4149444226); # 0xf7537e82 d = II(d, a, b, c, x[11], S42, 3174756917); # 0xbd3af235 c = II(c, d, a, b, x[ 2], S43, 718787259); # 0x2ad7d2bb b = II(b, c, d, a, x[ 9], S44, 3951481745); # 0xeb86d391 state[0] = (state[0] + a) % (2 ^ 32); state[1] = (state[1] + b) % (2 ^ 32); state[2] = (state[2] + c) % (2 ^ 32); state[3] = (state[3] + d) % (2 ^ 32); } for (i = j = 0; j < 16; j += 4) { digest[j + 0] = bw_and(state[i], 255); # 0xff digest[j + 1] = bw_and(bw_rshift(state[i], 8), 255); # 0xff digest[j + 2] = bw_and(bw_rshift(state[i], 16), 255); # 0xff digest[j + 3] = bw_and(bw_rshift(state[i++], 24), 255); # 0xff } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); return ret; } function F(x, y, z) { return bw_or(bw_and(x, y), bw_and(bw_not(x), z)); } function G(x, y, z) { return bw_or(bw_and(x, z), bw_and(y, bw_not(z))); } function H(x, y, z) { return bw_xor(x, bw_xor(y, z)); } function I(x, y, z) { return bw_xor(y, bw_or(x, bw_not(z))); } function FF(a, b, c, d, x, s, ac) { a = (a + F(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); a = (a + b) % (2 ^ 32); return a; } function GG(a, b, c, d, x, s, ac) { a = (a + G(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); a = (a + b) % (2 ^ 32); return a; } function HH(a, b, c, d, x, s, ac) { a = (a + H(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); a = (a + b) % (2 ^ 32); return a; } function II(a, b, c, d, x, s, ac) { a = (a + I(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); a = (a + b) % (2 ^ 32); return a; } function ROTATE_LEFT(x, n) { return bw_or((bw_lshift(x, n)) % (2 ^ 32), bw_rshift(x, 32 - n)); } function bw_not(x) { return bw_xor(x, 4294967295); # 0xffffffff } function bw_lshift(x, n) { return x * (2 ^ n); } function bw_rshift(x, n) { return int(x / (2 ^ n)); } function bw_and(x, y, i, r) { for (i = 0; i < 32; i += 4) { r = r / (2 ^ 4) + bw_lookup["and", x % 16, y % 16] * (2 ^ 28); x = int(x / (2 ^ 4)); y = int(y / (2 ^ 4)); } return r; } function bw_or(x, y, i, r) { for (i = 0; i < 32; i += 4) { r = r / (2 ^ 4) + bw_lookup["or", x % 16, y % 16] * (2 ^ 28); x = int(x / (2 ^ 4)); y = int(y / (2 ^ 4)); } return r; } function bw_xor(x, y) { return (x + y - 2 * bw_and(x, y)); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } function _bitwise_init( a, b, x, y, i) { # generate the bw_lookup table used by bw_and() and bw_or(). for (a = 0; a < 16; a++) { for (b = 0; b < 16; b++) { x = a; y = b; for (i = 0; i < 4; i++) { bw_lookup["and", a, b] += ((x % 2) && (y % 2)) * (2 ^ i); bw_lookup["or", a, b] += ((x % 2) || (y % 2)) * (2 ^ i); x = int(x / 2); y = int(y / 2); } } } } function _md5_init() { # MD5 shift constants setup. S11 = 7; S12 = 12; S13 = 17; S14 = 22; S21 = 5; S22 = 9; S23 = 14; S24 = 20; S31 = 4; S32 = 11; S33 = 16; S34 = 23; S41 = 6; S42 = 10; S43 = 15; S44 = 21; } |
diff -u step6.awk step7.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 | --- step6.awk 2017-03-04 12:57:02.936165000 +0100 +++ step7.awk 2017-03-07 12:08:08.666000000 +0100 @@ -57,7 +57,7 @@ hi = bw_rshift(nbytes * 8, 32); lo = (nbytes * 8) - bw_lshift(hi, 32); words[nwords++] = lo; - words[nwords++] = mod32bits(hi); # truncate to 32 bits + words[nwords++] = hi % (2 ^ 32); # truncate to 32 bits # Step 3. Initialize MD Buffer state[0] = 1732584193; # 0x67452301 @@ -145,10 +145,10 @@ c = II(c, d, a, b, x[ 2], S43, 718787259); # 0x2ad7d2bb b = II(b, c, d, a, x[ 9], S44, 3951481745); # 0xeb86d391 - state[0] = mod32bits(state[0] + a); - state[1] = mod32bits(state[1] + b); - state[2] = mod32bits(state[2] + c); - state[3] = mod32bits(state[3] + d); + state[0] = (state[0] + a) % (2 ^ 32); + state[1] = (state[1] + b) % (2 ^ 32); + state[2] = (state[2] + c) % (2 ^ 32); + state[3] = (state[3] + d) % (2 ^ 32); } for (i = j = 0; j < 16; j += 4) { @@ -179,39 +179,35 @@ } function FF(a, b, c, d, x, s, ac) { - a = mod32bits(a + F(b, c, d) + x + ac); + a = (a + F(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); - a = mod32bits(a + b); + a = (a + b) % (2 ^ 32); return a; } function GG(a, b, c, d, x, s, ac) { - a = mod32bits(a + G(b, c, d) + x + ac); + a = (a + G(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); - a = mod32bits(a + b); + a = (a + b) % (2 ^ 32); return a; } function HH(a, b, c, d, x, s, ac) { - a = mod32bits(a + H(b, c, d) + x + ac); + a = (a + H(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); - a = mod32bits(a + b); + a = (a + b) % (2 ^ 32); return a; } function II(a, b, c, d, x, s, ac) { - a = mod32bits(a + I(b, c, d) + x + ac); + a = (a + I(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); - a = mod32bits(a + b); + a = (a + b) % (2 ^ 32); return a; } function ROTATE_LEFT(x, n) { - return bw_or(mod32bits(bw_lshift(x, n)), bw_rshift(x, 32 - n)); -} - -function mod32bits(x) { - return bw_and(x, 4294967295); # 0xffffffff + return bw_or((bw_lshift(x, n)) % (2 ^ 32), bw_rshift(x, 32 - n)); } function bw_not(x) { |
% time gawk -f step7.awk sqlite-src-3160200/src/* | tee /tmp/step7.out
...
gawk -f step7.awk sqlite-src-3160200/src/* 225.86s user 0.20s system 99% cpu 3:46.08 total
tee /tmp/step7.out 0.00s user 0.00s system 0% cpu 3:46.08 totalAgain, about 35% faster and arguably a bit more readable too.
ROTATE_LEFT
By taking a look at ROTATE_LEFT, we see that we can use addition
instead of OR'ing between the high and low part of the result, because there
is no "overlap" between the operands "interesting bits" (i.e. no chance of
carry). In other words, addition and OR in this particular case will yield
the same result (but the addition will be faster than our slow
bw_or implementation).
We can apply this logic in a few other places and also to bw_and
by using modulo instead when we only care about the last few bits:
step8.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 | BEGIN { _ord_init(); _bitwise_init(); _md5_init(); } { # NOTE: remember the input files in-order in the `files' array. if (nfiles == 0 || files[nfiles] != FILENAME) files[++nfiles] = FILENAME; # XXX: only work with files ending with a newline, this is an OK # limitation since it is required by POSIX. content[FILENAME] = content[FILENAME] $0 "\n"; } END { # go over all the files in-order. for (i = 1; i <= nfiles; i++) { fn = files[i]; # a-la `openssl md5' output. printf("MD5(%s)= %s\n", fn, md5(content[fn])); } } # our md5 implementation function md5(input, nbytes, chars, i, bytes, hi, lo, words, nwords, state, a, b, c, d, j, x, digest, ret) { # convert the input into an array of bytes using ord() on each # character. nbytes = split(input, chars, ""); for (i = 1; i <= nbytes; i++) bytes[i] = ord(chars[i]); # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { hi = bw_lshift(bytes[i + 3], 8) + bytes[i + 2]; lo = bw_lshift(bytes[i + 1], 8) + bytes[i + 0]; words[nwords++] = bw_lshift(hi, 16) + lo; } # Step 1. Append Padding Bits if (nbytes % 4 == 0) { # the input size is congruent modulo 32, we need a new word to # store the first '1' padding bit. words[nwords++] = 128; # 0x80 } else { # append a '1' bit in the byte just after the last input byte. words[nwords - 1] = words[nwords - 1] + bw_lshift(128, (nbytes % 4) * 8); # 0x80 } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. while ((nwords % 16) != 14) nwords++; # Step 2. Append Length hi = bw_rshift(nbytes * 8, 32); lo = (nbytes * 8) - bw_lshift(hi, 32); words[nwords++] = lo; words[nwords++] = hi % (2 ^ 32); # truncate to 32 bits # Step 3. Initialize MD Buffer state[0] = 1732584193; # 0x67452301 state[1] = 4023233417; # 0xefcdab89 state[2] = 2562383102; # 0x98badcfe state[3] = 271733878; # 0x10325476 # Step 4. Process Message in 16-Word Blocks # Process each 16-word block. for (i = 0; i < nwords; i += 16) { # Copy block i into x. for (j = 0; j < 16; j++) x[j] = words[i + j]; a = state[0]; b = state[1]; c = state[2]; d = state[3]; # Round 1 a = FF(a, b, c, d, x[ 0], S11, 3614090360); # 0xd76aa478 d = FF(d, a, b, c, x[ 1], S12, 3905402710); # 0xe8c7b756 c = FF(c, d, a, b, x[ 2], S13, 606105819); # 0x242070db b = FF(b, c, d, a, x[ 3], S14, 3250441966); # 0xc1bdceee a = FF(a, b, c, d, x[ 4], S11, 4118548399); # 0xf57c0faf d = FF(d, a, b, c, x[ 5], S12, 1200080426); # 0x4787c62a c = FF(c, d, a, b, x[ 6], S13, 2821735955); # 0xa8304613 b = FF(b, c, d, a, x[ 7], S14, 4249261313); # 0xfd469501 a = FF(a, b, c, d, x[ 8], S11, 1770035416); # 0x698098d8 d = FF(d, a, b, c, x[ 9], S12, 2336552879); # 0x8b44f7af c = FF(c, d, a, b, x[10], S13, 4294925233); # 0xffff5bb1 b = FF(b, c, d, a, x[11], S14, 2304563134); # 0x895cd7be a = FF(a, b, c, d, x[12], S11, 1804603682); # 0x6b901122 d = FF(d, a, b, c, x[13], S12, 4254626195); # 0xfd987193 c = FF(c, d, a, b, x[14], S13, 2792965006); # 0xa679438e b = FF(b, c, d, a, x[15], S14, 1236535329); # 0x49b40821 # Round 2 a = GG(a, b, c, d, x[ 1], S21, 4129170786); # 0xf61e2562 d = GG(d, a, b, c, x[ 6], S22, 3225465664); # 0xc040b340 c = GG(c, d, a, b, x[11], S23, 643717713); # 0x265e5a51 b = GG(b, c, d, a, x[ 0], S24, 3921069994); # 0xe9b6c7aa a = GG(a, b, c, d, x[ 5], S21, 3593408605); # 0xd62f105d d = GG(d, a, b, c, x[10], S22, 38016083); # 0x2441453 c = GG(c, d, a, b, x[15], S23, 3634488961); # 0xd8a1e681 b = GG(b, c, d, a, x[ 4], S24, 3889429448); # 0xe7d3fbc8 a = GG(a, b, c, d, x[ 9], S21, 568446438); # 0x21e1cde6 d = GG(d, a, b, c, x[14], S22, 3275163606); # 0xc33707d6 c = GG(c, d, a, b, x[ 3], S23, 4107603335); # 0xf4d50d87 b = GG(b, c, d, a, x[ 8], S24, 1163531501); # 0x455a14ed a = GG(a, b, c, d, x[13], S21, 2850285829); # 0xa9e3e905 d = GG(d, a, b, c, x[ 2], S22, 4243563512); # 0xfcefa3f8 c = GG(c, d, a, b, x[ 7], S23, 1735328473); # 0x676f02d9 b = GG(b, c, d, a, x[12], S24, 2368359562); # 0x8d2a4c8a # Round 3 a = HH(a, b, c, d, x[ 5], S31, 4294588738); # 0xfffa3942 d = HH(d, a, b, c, x[ 8], S32, 2272392833); # 0x8771f681 c = HH(c, d, a, b, x[11], S33, 1839030562); # 0x6d9d6122 b = HH(b, c, d, a, x[14], S34, 4259657740); # 0xfde5380c a = HH(a, b, c, d, x[ 1], S31, 2763975236); # 0xa4beea44 d = HH(d, a, b, c, x[ 4], S32, 1272893353); # 0x4bdecfa9 c = HH(c, d, a, b, x[ 7], S33, 4139469664); # 0xf6bb4b60 b = HH(b, c, d, a, x[10], S34, 3200236656); # 0xbebfbc70 a = HH(a, b, c, d, x[13], S31, 681279174); # 0x289b7ec6 d = HH(d, a, b, c, x[ 0], S32, 3936430074); # 0xeaa127fa c = HH(c, d, a, b, x[ 3], S33, 3572445317); # 0xd4ef3085 b = HH(b, c, d, a, x[ 6], S34, 76029189); # 0x4881d05 a = HH(a, b, c, d, x[ 9], S31, 3654602809); # 0xd9d4d039 d = HH(d, a, b, c, x[12], S32, 3873151461); # 0xe6db99e5 c = HH(c, d, a, b, x[15], S33, 530742520); # 0x1fa27cf8 b = HH(b, c, d, a, x[ 2], S34, 3299628645); # 0xc4ac5665 # Round 4 a = II(a, b, c, d, x[ 0], S41, 4096336452); # 0xf4292244 d = II(d, a, b, c, x[ 7], S42, 1126891415); # 0x432aff97 c = II(c, d, a, b, x[14], S43, 2878612391); # 0xab9423a7 b = II(b, c, d, a, x[ 5], S44, 4237533241); # 0xfc93a039 a = II(a, b, c, d, x[12], S41, 1700485571); # 0x655b59c3 d = II(d, a, b, c, x[ 3], S42, 2399980690); # 0x8f0ccc92 c = II(c, d, a, b, x[10], S43, 4293915773); # 0xffeff47d b = II(b, c, d, a, x[ 1], S44, 2240044497); # 0x85845dd1 a = II(a, b, c, d, x[ 8], S41, 1873313359); # 0x6fa87e4f d = II(d, a, b, c, x[15], S42, 4264355552); # 0xfe2ce6e0 c = II(c, d, a, b, x[ 6], S43, 2734768916); # 0xa3014314 b = II(b, c, d, a, x[13], S44, 1309151649); # 0x4e0811a1 a = II(a, b, c, d, x[ 4], S41, 4149444226); # 0xf7537e82 d = II(d, a, b, c, x[11], S42, 3174756917); # 0xbd3af235 c = II(c, d, a, b, x[ 2], S43, 718787259); # 0x2ad7d2bb b = II(b, c, d, a, x[ 9], S44, 3951481745); # 0xeb86d391 state[0] = (state[0] + a) % (2 ^ 32); state[1] = (state[1] + b) % (2 ^ 32); state[2] = (state[2] + c) % (2 ^ 32); state[3] = (state[3] + d) % (2 ^ 32); } for (i = j = 0; j < 16; j += 4) { digest[j + 0] = state[i] % (2 ^ 8); digest[j + 1] = bw_rshift(state[i], 8) % (2 ^ 8); digest[j + 2] = bw_rshift(state[i], 16) % (2 ^ 8); digest[j + 3] = bw_rshift(state[i++], 24) % (2 ^ 8); } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); return ret; } function F(x, y, z) { return bw_or(bw_and(x, y), bw_and(bw_not(x), z)); } function G(x, y, z) { return bw_or(bw_and(x, z), bw_and(y, bw_not(z))); } function H(x, y, z) { return bw_xor(x, bw_xor(y, z)); } function I(x, y, z) { return bw_xor(y, bw_or(x, bw_not(z))); } function FF(a, b, c, d, x, s, ac) { a = (a + F(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); a = (a + b) % (2 ^ 32); return a; } function GG(a, b, c, d, x, s, ac) { a = (a + G(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); a = (a + b) % (2 ^ 32); return a; } function HH(a, b, c, d, x, s, ac) { a = (a + H(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); a = (a + b) % (2 ^ 32); return a; } function II(a, b, c, d, x, s, ac) { a = (a + I(b, c, d) + x + ac) % (2 ^ 32); a = ROTATE_LEFT(a, s); a = (a + b) % (2 ^ 32); return a; } function ROTATE_LEFT(x, n, l, r) { l = bw_lshift(x, n) % (2 ^ 32); r = bw_rshift(x, 32 - n); return (r + l); } function bw_not(x) { return bw_xor(x, 4294967295); # 0xffffffff } function bw_lshift(x, n) { return x * (2 ^ n); } function bw_rshift(x, n) { return int(x / (2 ^ n)); } function bw_and(x, y, i, r) { for (i = 0; i < 32; i += 4) { r = r / (2 ^ 4) + bw_lookup["and", x % 16, y % 16] * (2 ^ 28); x = int(x / (2 ^ 4)); y = int(y / (2 ^ 4)); } return r; } function bw_or(x, y, i, r) { for (i = 0; i < 32; i += 4) { r = r / (2 ^ 4) + bw_lookup["or", x % 16, y % 16] * (2 ^ 28); x = int(x / (2 ^ 4)); y = int(y / (2 ^ 4)); } return r; } function bw_xor(x, y) { return (x + y - 2 * bw_and(x, y)); } # from https://www.gnu.org/software/gawk/manual/html_node/Ordinal-Functions.html function _ord_init( i) { for (i = 0; i < 256; i++) _ord_[sprintf("%c", i)] = i; } function ord(s) { # only first character is of interest return _ord_[substr(s, 1, 1)]; } function _bitwise_init( a, b, x, y, i) { # generate the bw_lookup table used by bw_and() and bw_or(). for (a = 0; a < 16; a++) { for (b = 0; b < 16; b++) { x = a; y = b; for (i = 0; i < 4; i++) { bw_lookup["and", a, b] += ((x % 2) && (y % 2)) * (2 ^ i); bw_lookup["or", a, b] += ((x % 2) || (y % 2)) * (2 ^ i); x = int(x / 2); y = int(y / 2); } } } } function _md5_init() { # MD5 shift constants setup. S11 = 7; S12 = 12; S13 = 17; S14 = 22; S21 = 5; S22 = 9; S23 = 14; S24 = 20; S31 = 4; S32 = 11; S33 = 16; S34 = 23; S41 = 6; S42 = 10; S43 = 15; S44 = 21; } |
diff -u step7.awk step8.awk
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | --- step7.awk 2017-03-07 12:08:08.666000000 +0100 +++ step8.awk 2017-03-07 15:16:41.668779000 +0100 @@ -34,9 +34,9 @@ # convert the array of bytes into an array of 32-bits words. # NOTE: words is 0-indexed. for (i = 1; i <= nbytes; i += 4) { - hi = bw_or(bw_lshift(bytes[i + 3], 8), bytes[i + 2]); - lo = bw_or(bw_lshift(bytes[i + 1], 8), bytes[i + 0]); - words[nwords++] = bw_or(bw_lshift(hi, 16), lo); + hi = bw_lshift(bytes[i + 3], 8) + bytes[i + 2]; + lo = bw_lshift(bytes[i + 1], 8) + bytes[i + 0]; + words[nwords++] = bw_lshift(hi, 16) + lo; } # Step 1. Append Padding Bits @@ -46,7 +46,7 @@ words[nwords++] = 128; # 0x80 } else { # append a '1' bit in the byte just after the last input byte. - words[nwords - 1] = bw_or(words[nwords - 1], bw_lshift(128, (nbytes % 4) * 8)); # 0x80 + words[nwords - 1] = words[nwords - 1] + bw_lshift(128, (nbytes % 4) * 8); # 0x80 } # "fill" the remaining bytes with 0 until we're just shy two words of # having 16-Word Blocks. @@ -152,10 +152,10 @@ } for (i = j = 0; j < 16; j += 4) { - digest[j + 0] = bw_and(state[i], 255); # 0xff - digest[j + 1] = bw_and(bw_rshift(state[i], 8), 255); # 0xff - digest[j + 2] = bw_and(bw_rshift(state[i], 16), 255); # 0xff - digest[j + 3] = bw_and(bw_rshift(state[i++], 24), 255); # 0xff + digest[j + 0] = state[i] % (2 ^ 8); + digest[j + 1] = bw_rshift(state[i], 8) % (2 ^ 8); + digest[j + 2] = bw_rshift(state[i], 16) % (2 ^ 8); + digest[j + 3] = bw_rshift(state[i++], 24) % (2 ^ 8); } for (i = 0; i < 16; i++) ret = sprintf("%s%02x", ret, digest[i]); @@ -206,8 +206,10 @@ return a; } -function ROTATE_LEFT(x, n) { - return bw_or((bw_lshift(x, n)) % (2 ^ 32), bw_rshift(x, 32 - n)); +function ROTATE_LEFT(x, n, l, r) { + l = bw_lshift(x, n) % (2 ^ 32); + r = bw_rshift(x, 32 - n); + return (r + l); } function bw_not(x) { |
% time gawk -f step8.awk sqlite-src-3160200/src/* | tee /tmp/step8.out
...
gawk -f step8.awk sqlite-src-3160200/src/* 159.22s user 0.20s system 99% cpu 2:39.42 total
tee /tmp/step8.out 0.00s user 0.00s system 0% cpu 2:39.42 total30% faster although this was a tricky patch. Overall we've made very good progress on performances, going from about nine minutes to two and a half.
Wrap-up
At that point I am happy with the result. I guess it could be even more optimized but I'm not sure where to start (we could inline more functions as we've seen that function call are costly but that will come with a heavy readability penalty).
Through this post we've implemented MD5 from the RFC in GNU Awk to simplify the problem at first, then refactored the code to port it to "standard" AWK, and finally made optimizations. You can also find the full code on GitHub. Thank you for reading and I hope you had as much fun as I did :)